
Universidade Fernando Pessoa
Porto, Portugal

Turbidite Systems in Hydrocarbon Exploration
Turbidity currents, which create turbidite deposits, occur on time scales ranging from minutes to days. In contrast, in any location, the time between successive depositional events is thought to be on order of years to thousand years. Therefore, when studying turbidites, we are dealing with intermittent, punctuated equilibrium events. So before going on, let’s review the meaning and timing duration of a geological event (fig. 10).

Fig. 10- Geological events have been classified in (i) Regular, when the number of years necessary to have 95% chance that it takes place at least once is, roughly, 100, that is to say a century, (ii) Common, when the number of years necessary to have 95% of chances that it takes place at least once is around 1000 years, (ii) Recurrent, when it happens every millions years, (iv) Occasional, when it occurs every 10 M years and (v) Rare, when it occurs every 1G years (one billion years).
At the human scale, that is to say, two or three generations, low probable geological events are considered as possible, even if there is any natural law forbidding them. In the same way, there is no law forbidding that if you throw eight dice you get eight sixes. It is just a question of scale. Geologists know that what at the human scale is considered impossible it is only improbable at geological scale (condition “sina qua non” to understand geological systems). Indeed, using an 8 dice game, one can say:
“If you consider that every six of a die represents a geological agent, such a storm, a hurricane, an earthquake, a turbidity current, etc., you can make the hypothesis that a result of 7 six (throwing eight dice) represents an event less dramatic that the one produced by a result of 8 six. Also, a result of 5 six will be even less dramatic and more frequent than a result of 7, etc.”
It was using such reasoning that Gretener (1967) proposed a classification for discontinuous geological events (fig. 10). Indeed, taking into account such a classification, in geological history, two major families of geological events can be proposed:
i) Frequent events
Those which take place at least once 100 My and have time-duration of around 1 My, that is to say, 1/100 of total time (fig. 11).
ii) Rare events
Those which take place at least once 1,000 My with a time-duration of around 10 My (see fig. 11).
In this sense, a turbidite-current (gravity current in a “lato sensu”) is a regular or common geological event. In a particular basin, its occurrence-time ranges between 1 and 5,000 years. In other words, a turbidity current is not a rare geological event, i.e. is a punctual geological episode with a low rate of renewal in the Earth’s history (2-5 times). In addition, it must be noticed that an instantaneous geological event, such as turbidity current, is a relative concept. Actually, taking into account deep-geological time, the time-duration of a geological event is always a relative concept, as illustrated on fig. 11.
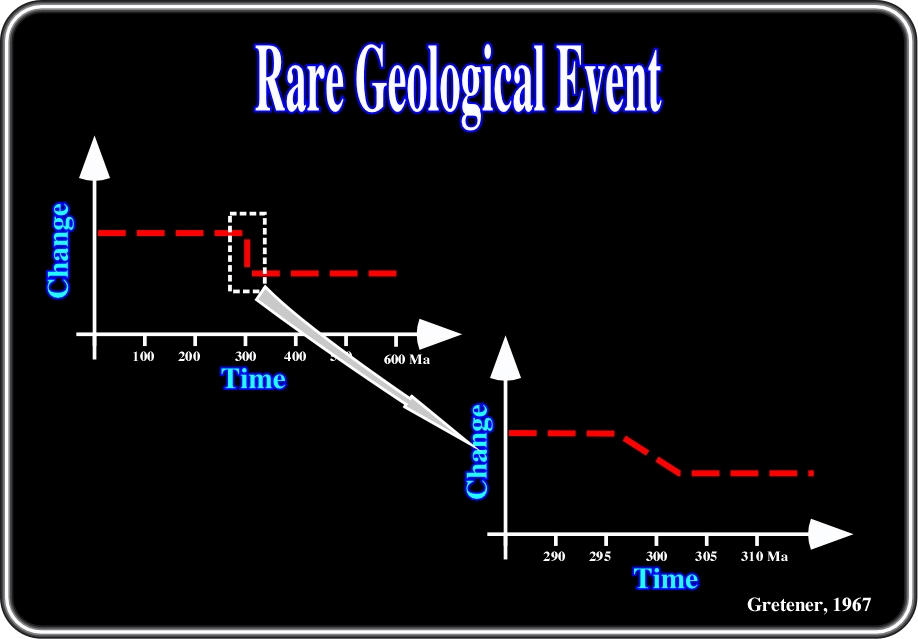
Fig. 11- At a geologic scale (on the left in the figure), a Paleozoic geological event, such as a sequence stratigraphic cycle, induced by a 3rd order eustatic cycle, which time duration ranges between 0.5 and 3-5 My, is an instantaneous geological event. Its time-duration (3-5 My) is approximately 1/100 of the total time of the Phanerozoic. However, in a dilated time-scale (on the right), the same event has a finite time-duration of 6 My.
Mathematically, an instantaneous event is characterized by a time-duration exceeding barely 1/100 of total time. Such a concept, when expressed diagrammatically, in change versus time, as depicted in fig. 9, the changing time corresponds just to the thickness of the pencil line. Knowing the time-duration of geological events and the directly or indirectly associated deposits, geologists always must take into account the completeness and preservation of sedimentary records. The subject of completeness and the preservation of the turbidite deposits, as discussed next, is quite important to the understanding of turbidite systems.
III) Completness and Preservation
For a long time, geologists asked themselves the key question regarding the continuity versus discontinuity of geologic events:
Are sedimentary records the result of more or less continuous geologic processes, or are they the result of extraordinary processes, which take place in a spasmodic way?
Since the 18th century, geologists have given very opposite answers. Presently, the majority of them consider that sedimentary records are incomplete and separated by important periods of non-deposition during which nothing happens. It is then surprising to see some geologists continue to forget in their stratigraphic models the long periods of non-deposition during which nothing happens. In fact, in stratigraphic sections, the time-duration of hiatuses (by non-deposition or erosion) generally represent much more time than the deposition-time of the preserved sediments.
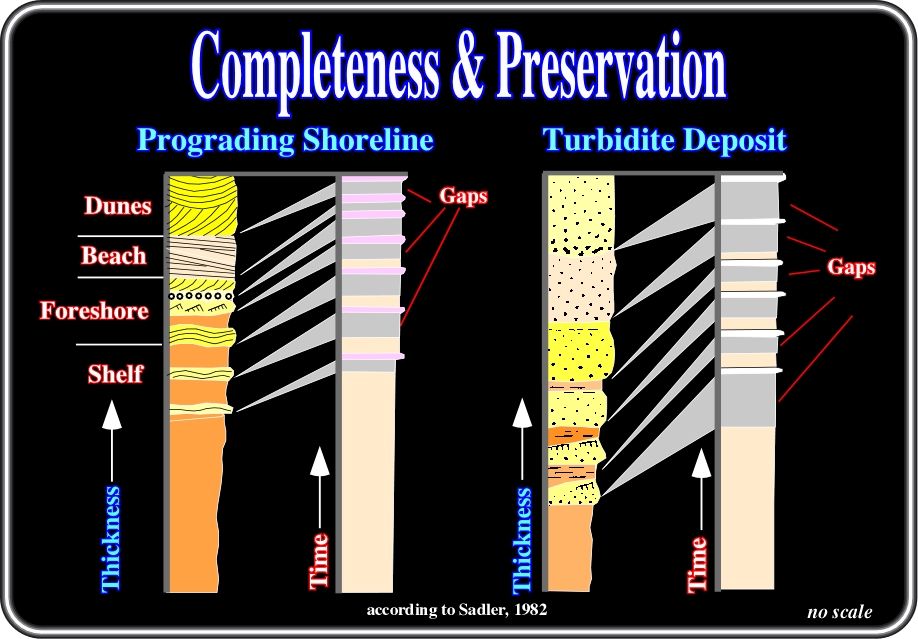
Fig. 12- In these geological cross-sections, and particularly on their upper parts, the periods of non-deposition are much longer than the periods of deposition. In the prograding shoreline cross-section, illustrated above, a large number of geological events took place, but the associated deposits are not preserved. They have been eroded. They were replaced by significant erosional-hiatuses. In the turbidite cross-section, erosion is insignificant. The hiatuses are non-depositional. The sedimentary preservation is much higher than in the prograding shoreline cross-section, however, conversely the completeness is much lower (see text below).
Stratigraphic sections are just local archives of geologic history (Sadler, 1982). The records of these archives are the sedimentary layers. They are deposited in succession and, generally, numbered according to their thickness rather than their deposition-time (period during which there is deposition). Nevertheless, geologists have long known that stratigraphic sections contain numerous hiatuses induced by either erosion or non-deposition (fig. 12). On this particular subject, three important questions often come to the mind of geologists:
1) What is the deposition-time of a single sedimentary bed?
2) What is the total time of deposition of a stratigraphic section, that is to say, the span of time between the bounding unconformities?
3) What is the ratio between the total time of a section and the actual deposition-time of its beds?Concerning the first question one can say that:
1.1) A lamination of a beach deposit is deposited in about one second.
1.2) A HCS bed (“hummocky cross stratification“), characteristic of a storm deposit, is deposited in few minutes.
1.3) A turbidite layer is deposited in a few hours.
1.4) A flood deposit, such as the Scablands in Canada (deposits, and erosions, associated to the floods induced by the break-up of the lake’s retentions at the back of Plio-Pleistocene glaciers), can be deposited in few weeks.
1.5) A glacial varve is deposited in 1 year.
1.6) A centimetre of a pelagic sediment is deposited during about 100 years.Concerning, the second question we can say that:
2.1) A continental encroachment stratigraphic sub-cycle has a time-duration ranging between 10 and 20 million years (Duval et al., 1993);
2.2) A continental encroachment stratigraphic cycle has a time-duration ranging between 100 and 300 million years (Duval et al., 1993).Sadler (1982) suggested that deposition-time is conversely proportional to the rate of deposition. Higher the rate the shorter the time. From such a hypothesis, it follows that the majority of periods of non-deposition escape us. The sedimentary records corresponds to short periods of terror separated by long periods of tranquillity where nothing happen (Ager, 1982).
The last question, i.e. what is the ratio between the total time of a stratigraphic section (span of time between the bounding unconformities) and the deposition-time of all its preserved beds? This is more difficult to answer. It puts forward the problem of the completeness of stratigraphic section, i.e. the deposition-time and the preservation of the beds composing a section. The preservation of a stratigraphic section generally depends on:
(i) The amplitude.
(ii) The frequency of the stratigraphic events.
(iii) The depositional environment.The stratigraphic events more represented in the stratigraphic records are those that have a normal or weak frequency, i.e. those that take place sporadically. In this sense, basin floor and slope fans strongly contrast with pelagic shaly intervals, which separate them (fig 13). The pelagic intervals are stratigraphic events with normal frequency, whereas turbidite deposits are instantaneous low frequency events.

Fig. 13- Each bed represents a Turbidite. Here, the turbidites are made up of sandstone. Between each one, there are pelagic-layers, which represent the argillaceous deposits resulting from the sedimentation of suspension in the basin. In terms of time, the turbidites represent instantaneous deposits (a few hours), while the pelagic deposits represent hundreds, even thousands of years.
Let’s see an example:
a) Suppose an interval composed by 100 turbidite layers and 100 layers of pelagic clays.
- Each turbidite-layer has a thickness of 10 cms,
- Each pelagic-layer has a thickness of 5 cms,
b) The total thickness will be 1500 cms.
c) Assuming an average depositional rate of the pelagic clays of 5 cms / 1000 years, and
d) A depositional rate of the each turbidite-layer as instantaneous.
Subsequently, one can deduct:
(i) The total-deposition time is 100,000 years.
(ii) The frequency of turbidity currents is 1000 years.
(iii) The completeness and the preservation of the pelagic clays is 1.
(iv) The completeness of the turbidite layers is almost zero (0), but its preservation is 1, i.e. almost total (Dott, 1983).In addition, when dealing with intermittent, punctuated equilibrium phenomenon, by studying the thickness of layers, ranging from centimeters to several meters, one can estimate the distribution of currents (avalanches) causing the sedimentation (Bak, 1999), as illustrated in fig. 14.
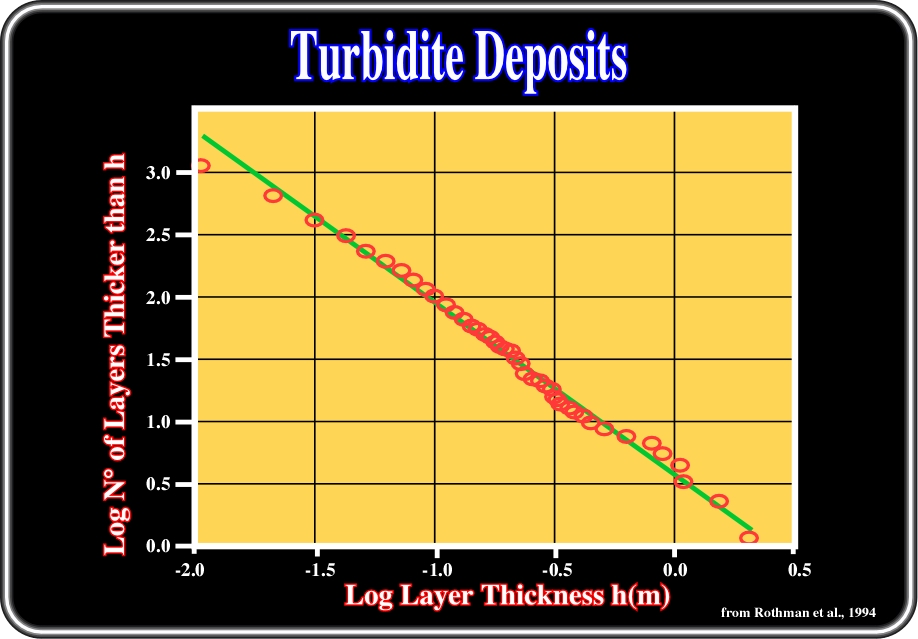
Fig. 14- Nature is characterized by self-similarity. Natural objects, or natural events, have a fractal geometry and so, when listed in decreasing size and plotted on a log-log format with size against rank show a fractal distribution (parabolic or not). Indeed, turbiditic deposition exhibits a punctuated equilibrium behaviour, where periods of stasis are interrupted by intermittent sandprone gravity currents. Such a behaviour is expressed by a straight line on a double logarithmic plot, as illustrated above, which indicates that the number of events can be given by a simple power law. This plot, proposed by Rothman (1994) for 1235 turbidite layers (with a thickness higher than h) observed in the Kingston peak formation (Upper Proterozoic, southern Panamint Range in eastern California). The straight line has a slope of 1.39, which indicates a power law distribution of the thickness of the layers and thus the distribution of the turbiditic currents forming them.
Finally, from this example we can conclude:
Two thirds of the sedimentary interval was deposited by instantaneous events with a low frequency (one event each thousand years). In 10 My, ten thousand (10.000) instantaneous turbidite-events have deposited a section of 1500 meters. In other words, what seems impossible at the human scale becomes, on a geological scale, possible, and the improbable becomes inevitable (Simpson, G. G., 1952).
Generally speaking, a turbidite is a sedimentary rock deposited from, or inferred to have been deposited from a turbidity current. The term turbidity current was introduced by Johnson, D. W. (1939) and applied to a current due to turbidity and not to one showing that property. Such a current can be defined as a density current in water (air or other fluid) caused by different amounts of matter in suspension (fig. 15).

Fig. 15- The easiest way to describe a turbidity current is an underwater avalanche - imagine the cloud of snow and ice that accompanies a snow avalanche as it cascades down a mountainside (right). Turbidity currents are a bit like that cloud, but they are composed of sediment grains and occur under the sea. When a submarine landslide is triggered, some of the sea floor sediment is picked up by turbulent currents created by the landslide. This current (known as a turbidity current because of its turbulent nature) races downslope towards the deep ocean, carrying its sediment load along with it. As the current begins to slow down, it no longer has the energy to carry its load of sediment, and the particles start to settle out onto the sea floor, forming a turbidite deposit (http://www.soc.soton.ac.uk/CHD/classroom@sea/general_science/turbidites.html).
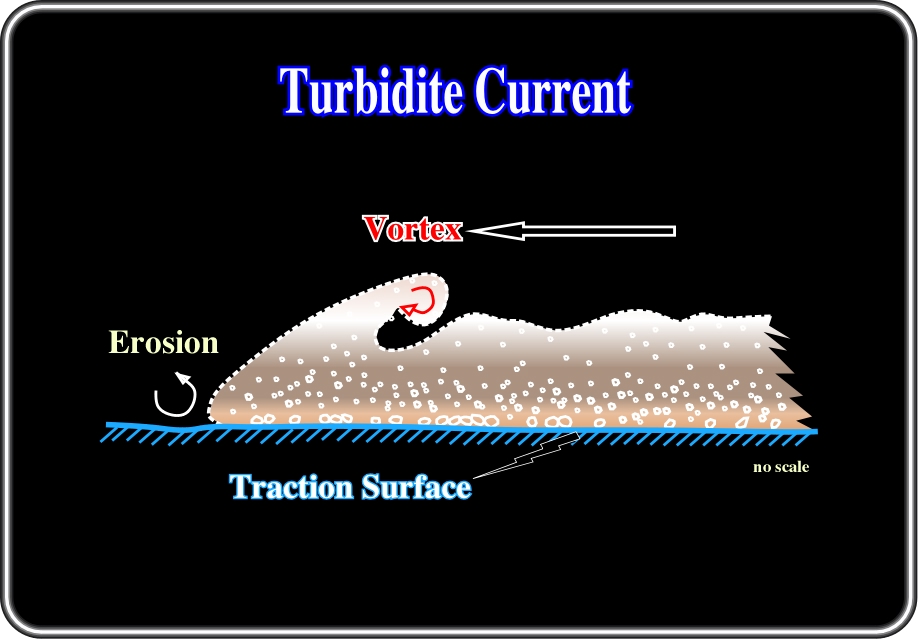
Fig. 16- In turbidity currents, the majority of the material is transported by the mechanism depicted above. They can travel hundreds of kilometres at relatively high velocity (dozens of km/h). In the frontal part of a current, there is erosion by aspiration, and deposition after its passage. Large blocks travel by traction the bottom, while the smaller particles stay in suspension.
Specifically, a turbidity current can be defined as a bottom-flowing current laden with suspended sediment, moving swiftly (under the influence of gravity) down a sub-aqueous slope and spreading horizontally on the sediment surface, having been set and /or maintained in motion by locally churned or stirred-up sediment that gives the flow a density greater (fig. 17) than that of the surrounding or overlying clear water (Bates R. L. & Jackson, J., 1980).
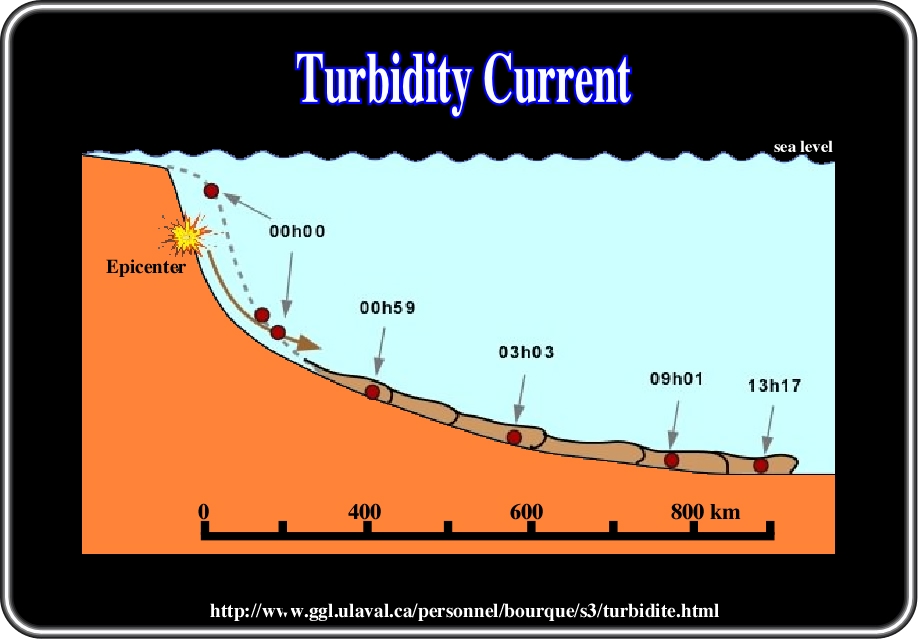
Fig. 17- The very large gravity flow, which took place on November 18, 1929 in Great Banks of Newfoundland, is a good example to understand the mechanism of sediment transportation. The speed and the progression of this gravity flow were particularly well documented thanks to the rupture of underwater telegraphic cables, which rested on the sea bottom. An earthquake whose epicentre was located on the South Newfoundland continental slope caused a gigantic landslide which put in suspension tons of sediments forming a dense turbiditic current, which ran out on the sea-bed and spread out a distance of more than 800 km over the abyssal plain of Sohm. All the underwater cables in the sector of the earthquake were broken instantaneously. The other cables, more distant, were cut as they were mown by the current of turbidity. The progression of the current is indicated by the hour to which each cable was broken (for the purpose of demonstration, time 00h00 on the diagram corresponds to the release of the current). The maximum speed of the current was evaluated at 95 km/h. Approximately 100 km3 of sediments were transported and deposited on a surface of 100 000 km2 in only one layer of a few centimetres thickness. Such a layer is what geologists call a turbidite. The repetition of such events during the life of a continental terrace (several million years) build thick sedimentary sequences containing thousands of turbidites.
Turbidity currents occur in lakes and seas. They can produce sub-aqueous canyons by notching the slopes before deposing at their bottom the laden sediments as sub-aqueous fans. Turbidity currents can originate in various ways (fig. 18), such as:
- Storm waves;
- Tsunamis;
- Earthquake-inducing sliding;
- Eustatic sea fall;
- Tectonic movements;
- Slope instabilities;
- Upwelling currents;
- Over-supply of sediments;
- Heavily charged rivers in spate with densities exceeding that of the sea water, etc, etc.

Fig. 18- Turbiditic currents can be triggered by a lot of geological events. Relative sea levels falls displacing seaward and basinward coastal onlaps, exhume the continental platform. The sediments are discharged on the upper slope and so transported downdip, toward the deep parts of the basin, where they are deposited as fans as soon as the competence of the currents decrease drastically. When the amplitude of the relative sea level fall is not big enough to completely exhume the platform, it requires the deltaic sandbodies to strongly prograde seaward, as depicted in photograph A. With so much sediment building up on the continental shelf, it is inevitable that the sea floor becomes unstable. Submarine landslides are quite common, triggered either by a sudden event such as an earthquake or simply by the sheer weight of sediment building up on the continental shelf. The size of such landslides varies hugely; larger landslides leave behind huge scars in the sea floor - steep cliffs rising even higher than those seen on land. Downslope from the scar, you might find evidence of the slide - enormous blocks of rock scattered across the sea floor like giant building blocks. The photograph B, illustrates a landslide scar resulting from an earthquake-induced landslide in California. The satellite image (photograph C) clearly shows sandy bedforms and seaweed on the Bahamas coast. Tides and ocean currents in the Bahamas sculpted the sand and seaweed beds often inducing the onset of turbidite currents. The 3D image of the Storegga slide scar (photograph D), in the offshore Norway, strongly corroborates the conjecture of a few geologists who consider the associated slide as one of the biggest ever, triggered probably by release of hydrocarbons under the sediment 7000 years ago.
All these geological events are catastrophic and discontinuous. They have a very different time-durations and all have complex behaviour and the tendency to create large Self-Organized Critically systems (SOCs). In fact, so far, shelf-organized critically is the only known general mechanism able to generate complexity (Bak. P., 1996). However, self-organized critically systems can be understood only from a holistic description of properties of the entire system. They cannot be understood from a reductionist description of the individual elements composing the system (as in the sandpile model of Bak, P., 1947).
In other words, turbidite systems are deposited by turdidity-currents and are complex geological systems. Most changes take place through catastrophic events. They do not follow a smooth gradual path. Subsequently turbidite deposits cannot be understood by just studying their different components, since the whole system is more than the simple addition of its parts.
to continue press
next