Porto, Portugal
Contents: 4.1- Scale Problems 4.2- Volume Problems in Compressional Tectonic Regimes (1 horizontal) 4.2.1- Compression---Shortening---Uplift---Erosion 4.2.2- Balanced Structural Interpretation 4.2.3- Depth to Detachment 4.2.4- Limitations of Depth to Detachment Calculations 4.2.5-Volume Conservation 4.2.6- Kink Method 4.2.7- Kink Software 4.2.8- Fault Propagation 4.2.9- Fault-bend Fold 4.2.10- Kink Method in Seismic Sections 4.3- Volume Problems in Extensional Regimes (
The Second Law of Thermodynamic when applied to geologic deformations is known as Goguel's Law (1952):
"Throughout deformation volume is conserved”
(except for that due to a loss porosity)
Nevertheless, in limestone facies, stylolithisation implies often a loss of volume over 20%. Goguel's Law is a volumetric law in a three-dimensional domain. Geological sections or seismic lines are two-dimensional.
Consequently, to use this law in geologic cross-section or in seismic interpretation, it is necessary simplify it by:
(a)- Using sections perpendiculars to tectonic trends (
(b)- Using the length of beds or seismic markers as a volume equivalent. In a concentric tectonic folding (hydrocarbon's domain), the volume of sediments can be correlated with the length of the beds. In other words the three-dimensional Goguel's Law becomes roughly a unidimensional law.
This law is only valid in geological cross-sections with the same vertical and horizontal scales (natural scale). One should not forget:
(i) the majority of cross-sections is vertically exaggerated,
(ii) conventional seismic lines are time sections.
(iii) seismic lines, on workstation's windows are, often, too much anamorphosed.
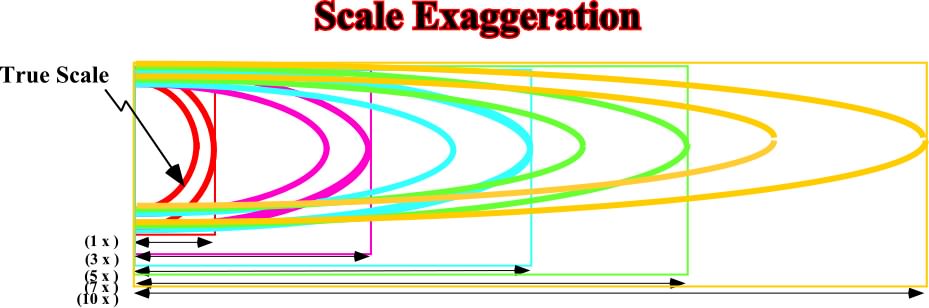
Fig. 85- Effects of vertical exaggeration on stratigraphic thickness and dips on beds of a unit thickness anticline anticline (from Sitter, 1974).
On time seismic lines the Goguel's Law is more than approximate. Nevertheless, it still is very useful to prevent inconsistent geological interpretations. The unmigrated seismic line, illustrated on fig. 86, having a vertical time scale and an horizontal metric scale gives only a rough idea of the geometry of the sediments. In fact, with such a seismic processing, the stratigraphy, tectonic behaviour and geometry of the fault planes is quite difficult to predict.
Fig. 86- Seismic lines are roughly time profiles. So, when interpreted, in geological terms, interpreters should not forget that Geology is scale dependent. In other words, interpreters must take into account not only the horizontal and vertical scales but lateral velocity changes as well. In addition, when working with unmigrated seismic data, as seismic horizons (chronostratigraphic lines) are not in its real position, the geometry and internal configuration of seismic interval must be carefully determined.
Migrated data strongly increases the geological evidence. Seismic profiles look more like a geological cross-section and so, the geometry of seismic intervals can be partially predicted in depth. Taking into account the main differences between a seismic line (time section) and a geological profile (depth section) is a fundamental step in seismic interpretation.
Conventional time migrated lines are generally vertically exaggerated. They have different vertical and horizontal scales. Therefore, they do not give an accurate picture of the sedimentary geometry. The dips of the chronostratigraphic markers are strongly enhanced and the thickness of the intervals can only be predicted knowing the interval velocity (fig. 87).
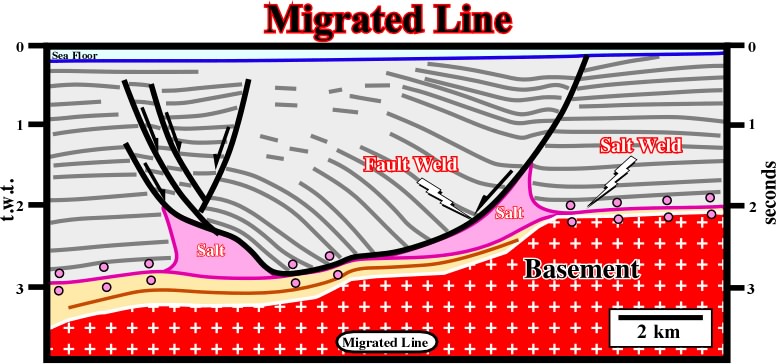
Fig. 87- The migrated version of the previous line, in spite of the fact that vertical scale is in time, has the appearance of a cross-section. The large majority of the diffractions has disappear. However, the seismic reflections are not in their really position and the lateral changes of velocity is not apparent. Therefore, the interval thicknesses and the dip are the reflections is apparent (compare with fig. 88).
On depth migrated lines, as that illustrated on fig. 88, when the vertical and the horizontal scales are the same, as in the field (natural scale 1 : 1), dips and interval's thickness are really. Nevertheless, even these seismic lines can present pitfalls related with deficient knowledge of lateral changes of interval's velocity or lateral arrivals.
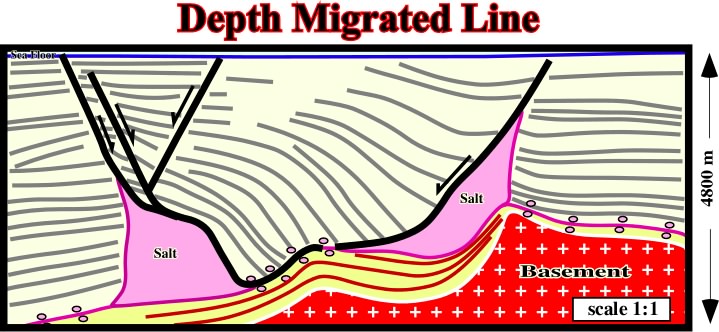
Fig. 88- On This seismic line lateral changes of the velocity induced either by thickness' variation of the evaporitic layer (high velocity) and/or the Tertiary depocenter (low velocity) are not adequately corrected. The bottom of the salt layer (or salt weld) should not be undulated but planar.
Geometrical relationships (onlap, downlap and toplap) between seismic reflectors (chronostratigraphic lines) and the non-conformities are strongly enhanced, as well as seismic surfaces (onlap, downlap and unconformities), when the vertical scale is exaggerated. On the contrary, the effect of vertical exaggeration of seismic lines (depth or time), which is the ruler in workstations' interpretations, mask the real geometry of reflections and fault planes. Indeed, as illustrated on fig. 89, the Anderson's law (dip of the faults) must be used carefully.
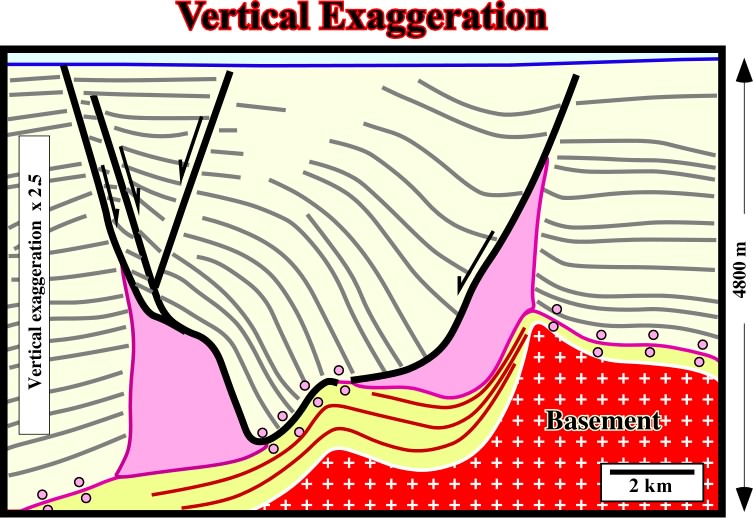
Fig. 89- On this vertically exaggerated version of the line illustrated on fig. 88, it is quite evident the undulations (seismic pitfall) of the bottom of the salt are too exaggerated. Similarly, the dips of the normal faults (stretching faults), associated with the apex of the antiform, are higher than predicted by Anderson's law. The same happens with the fault weld bordering the depocenter. It is interesting to notice the fault weld is underline by a seismic reflector. In fact, the fault gauge zone, is filled by salt, which creates a strong positive acoustical impedance contrast with the low-velocity sediments of the depocenter.
Conventional 2D seismic lines have a vertical scale in time (two way times) and a metric horizontal scale metric. Therefore, they give a slightly vertically exaggerated depiction of reality. In other words, the dips of the chronostratigraphic lines are always exaggerated. On the other hand, in offshore lines showing an significant seaward water depth increasing, as the line illustrated on fig. 90, the dips of the reflectors are also exaggerated due to the lateral change in velocity induced by the water-depth increasing.
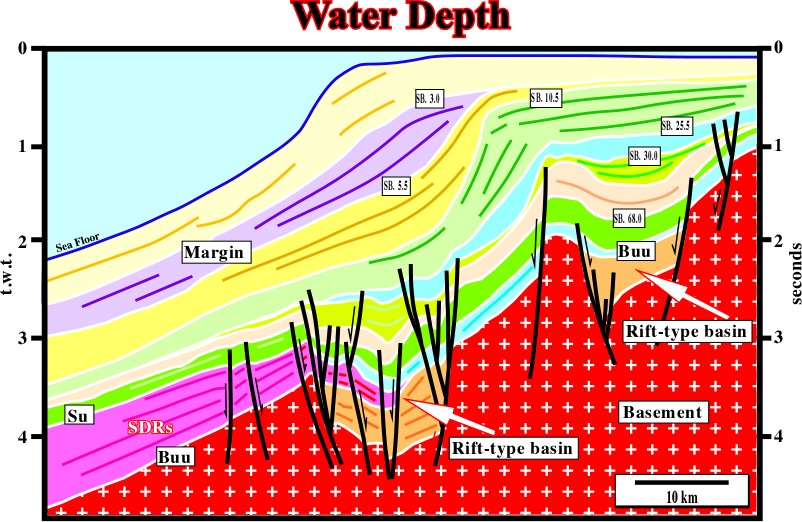
Fig. 90- On this line (western offshore India), due to the abrupt changing in water-depth (limit between the platform and upper continental slope) and, also, to the continuous seaward water-depth increasing, the apparent geometry of the reflectors is deformed. In fact, the seaward dip of the subaerial lava flows (SDRs, i.e. seaward dipping reflectors) is quite exaggerated, since the velocity of the seismic waves in the water is much lower than in sediments. Indeed, very often, in the distal areas of continental divergent margins (e.g. offshore Angola or Brazil), the geometry of the reflectors can be inversed; on a time seismic, the sediments dip seaward, but in time-depth conversion version, they dip landwards.
4.2- Volume Problems in Compressional Tectonic Regimes (1 horizontal)
4.2.1- Compression-------Shortening-------Uplift-----Erosion
During a compressional tectonic regime, the sediments are shortened and so be uplifted. The uplift creates a relative sea level fall, that is to say, an unconformity and subsequent erosion.
The shortening takes place along
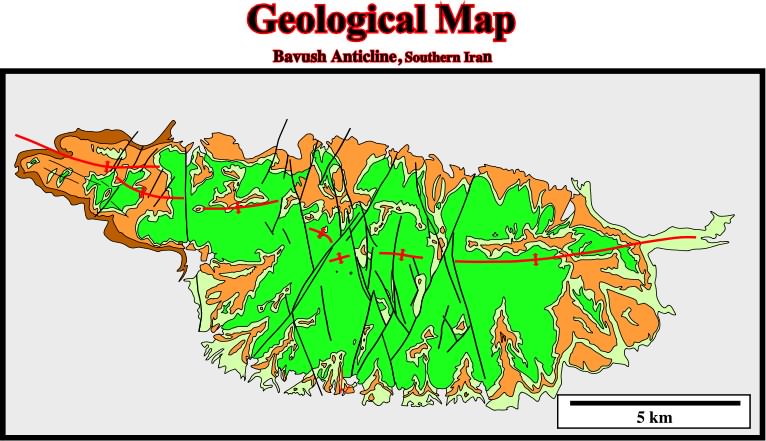
Fig. 91- The elongation the Bavush anticline (onshore Iran) along the
Subsequent, in such a areas of concentric folding, cross-sections can be are difficult to balance. In addition, as we see later, due to volume problems, the folds die in depth on a décollement surface.
4.2.2- Balanced Structural Interpretation
Balanced structural sections can be tested by palinspatic restoration. Balancing is a selective testing of restoration (scale 1:1). Computer-generated geological cross-section (fig. 92) can be made using input interpreted seismic lines, well-log and field data. The output can be a computer drafted coloured section small to large, based on flexural slip geometry.
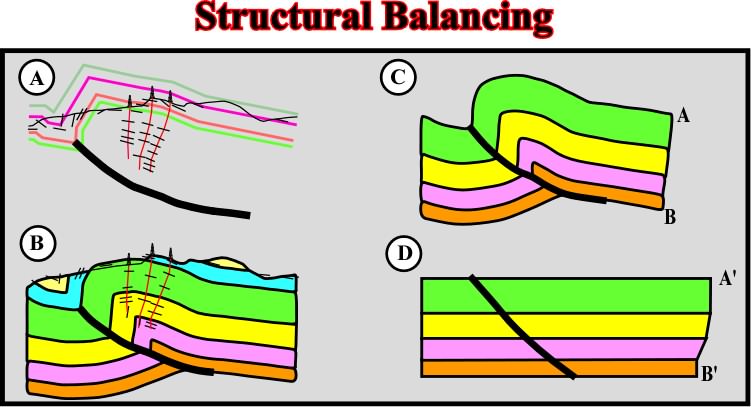
Fig. 92- Structural interpretations must respect the Goguel's law, they must be equilibrated, that is to say, the volume of sediments must be kept constant during deformation. So, in this particularly example, in which a geological cross-section was built using well-dipmeter results, the geometry of the reverse fault is paramount. Indeed, when unfolding the sediments, they must be displaced along the fault plan without creating voids (missing sediments) or overlapping (too much sediments).
The décollement level can be calculated by the excess of area method (fig. 93). The excess of area uplifted should be balanced by the area reduced by shortening.
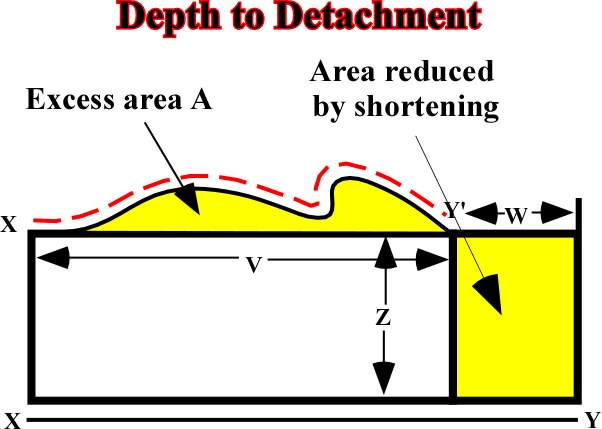
Fig. 93- Admittedly, in order to respect Goguel's law, the area A (excess area) must be equal to the area B (area reduced by shortening). Knowing the area A and the horizontal shortening W, which can easily be determined (W=XY-V), it is possible to determine the décollement depth Z. Indeed, Z =(area A)/W, since area A = Area B = WZ.
4.2.4- Limitations of Depth to Detachment Calculations
Detachment calculations assume:
- That a décollement exists.
- Constant tectonic transport in plane (
- No flowage.
Volume conservation (fig. 94) is respected by:
- Folding and décollement on underlying mobile layer (salt-shale).
- Folding and faulted basement or imbricated basement.
- Imbrication.
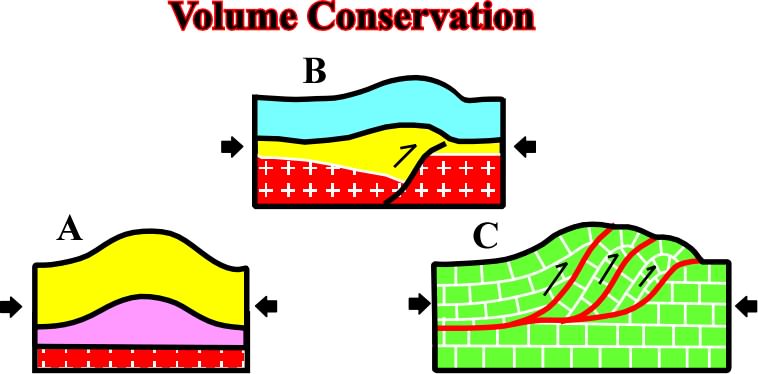
Fig. 94- In A, volume conservation is realized by folding and décollement on an underlying mobile layer (salt or shales). In B, volume conservation is realized by folding and faulted or imbricated basement; the pre-existent normal fault is reactivated, as reverse fault, during the compressional tectonic regime. Finally another way to respect the Goguel's law is imbrications, which generally develops in uniform competent sediments such as limestone's.
The kink method can be used to pick fault planes or to restore sections. However, it can be only used in compressional regime, because it supposes a bed-to-bed movement, which is generally not observed in extensional regime. This method can be presented in several basic steps:
- Location of regions of homogeneous dip.
- Location of axial surfaces between regions of homogeneous dip.
- Location discontinuities in structures where axial surfaces terminate .
- Interpretation of termination of axial surfaces in terms faulting.
The difference between kink band folds and folds formed above a décollement is illustrated below (fig. 95).
Fig. 95- The basal space problem of décollement kink bands can be explained by the importance of the mobile layer thickness. It may be schematically assumed that its compression is achieved by means of the elimination masses used to fill the basal triangular space of kink bands.
The following screen images (fig. 96- show the development of a structural interpretation from a well data base using the kink method (GSI, 1985). The problem is:
1) Locate the top of the footwall.
2) Determine the fault trajectory and the internal geometry of the hanging wall.
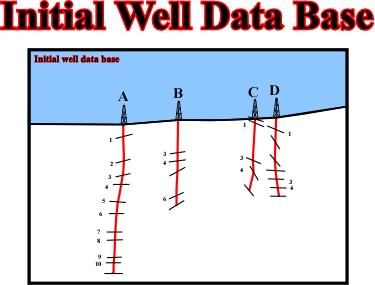
Fig. 96- The initial data base is given by the interpretation of the dipmeters logs and the stratigraphy of four wells. The profile A, B, C, D is perpendicular to the strike of the beds, so, the they are real dips.
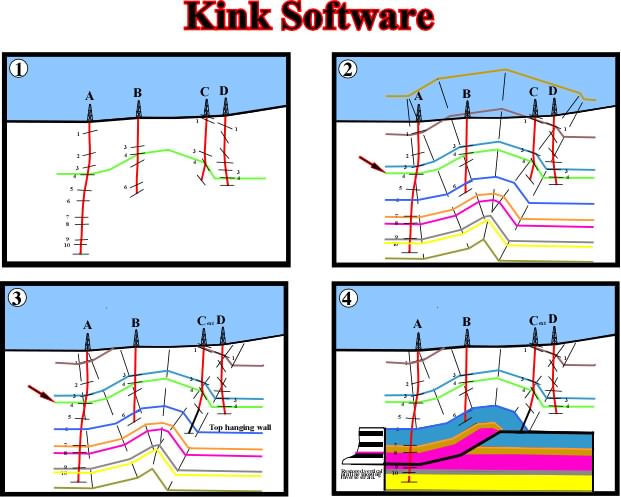
Fig. 97- Using dip projections an horizon is constructed through the top of 4 formation compatible with all dip information (step 1), then its geometry is projected above and below the constructed 4 top horizon to check data compatibility(2) and extended until the top of the hanging wall is located (2). Now the section can be quickly modified by projecting the detachment plane and leading thrust fault surface and by constructing the horse and its internal geometry (3); The horse is restored to examine the state of strain in the sheet (4).
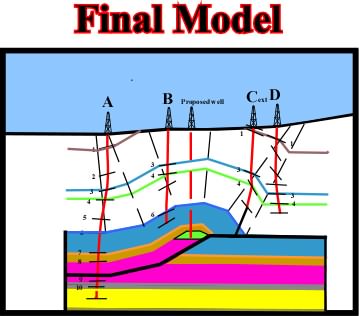
Fig.98- Finally, a complete new model with predicted horse is established, which implies a new strategy, that is to say, drill through top of predicted anticline to top of oil potential trap.
Fault propagation fold (fig. 99), kink method.
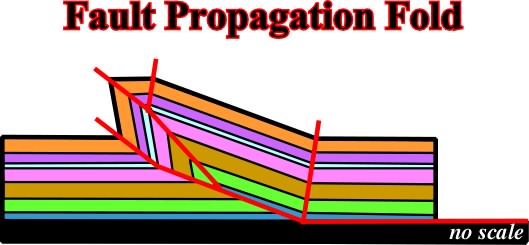
Fig. 99- In this model, the faults of the upthrown block die on a detachment plane. When an interpretation of this kind is proposed, geologist must be sure than volume problems are respected.
Fault-Bend fold (fig. 100), kink method.
Fig. 100- This model, quite similar to the previous one, require to be strongly critised when proposed in a geological interpretation, particularly of a seismic line.
The following schematic drawings show patterns of reflections on seismic sections that display kink folds.
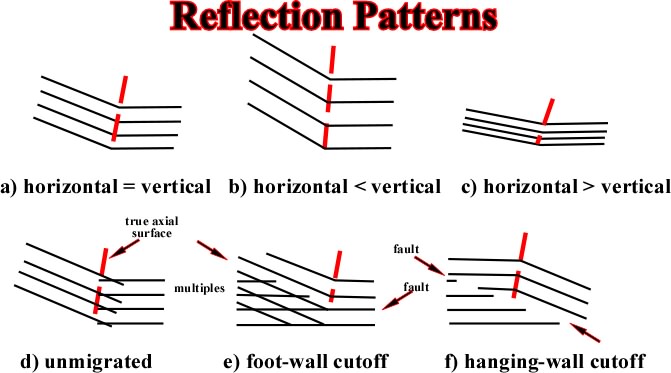
Fig. 101- When migrated seismic lines were not available, this method was quite usefull. Presently, as the large majority of the seismic lines are migrated, it becames obselet.
4.3- Volume Problems in Extensional Regimes (l vertical)
4.3.1- Extension------Subsidence-----RSL Rise-----Sedimentation
During an extensional tectonic regime, the sediments are lengthened. A lengthening implies subsidence, which creates a relative sea level rise, that is to say, an icreasing of accommodation (space available for sediments) and so sedimentation. However, geological features, such as isostatic factors, subduction of plates etc., can also produce subsidence and uplift. On the other hand, local crestal erosion is often associated to tilted blocks (extension).
In extension, volumes problems develop, in depth, a tectonic disharmony and a detachment, or décollement surface. The depth of such a surface can be determine using the excess area method.
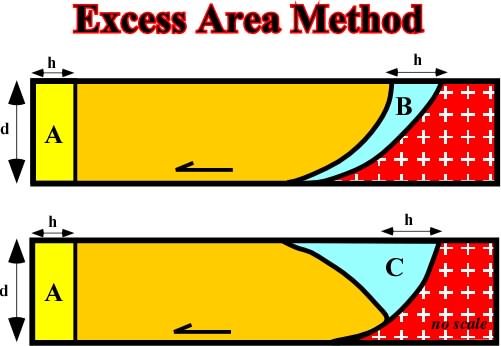
Fig.102- As during deformation the volume of sediments must be kept constant (no voids, or overlapping), in a cross-section oriented perpendicularly to the transportation axis, the area A is equal to area B and area C. Thus, knowing the heave of the fault, h, one can accesses de depth of detachment, d, by d= area C/h.
4.3.3- Normal Faults & Volume Problems
In absence of horizontal throw of the faults, planar and cylindrical faults (fig. 103) do not create important volume problems:
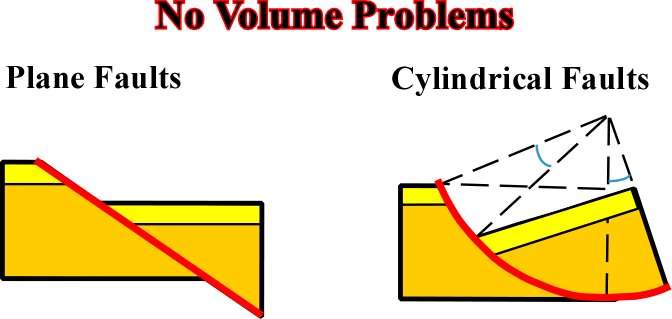
Fig. 103- In a planar fault there is translation and both faulted blocks have the same dip, so there is not significant volume problems. Similarly, in a cylindrical fault, the rotation of the hangingwall induce a different dip from the footwall, but there is no major volume problem.
However, other kinds of norma faults imply volume problems and certain accommodations are necessary (fig. 104).
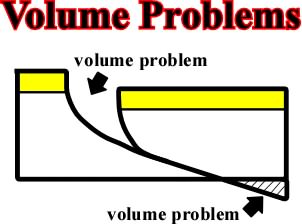
Fig. 104- In this example, without scale, a post-depositional extension creates two major problems: (i) a void and (ii) an overlapping. Subsequently, in order to respect Goguel's law, sediments must accommodate to the new space conditions.
4.3.4- Fault Curvature with Depth
Theoretical examples are illustrated on fig. 105.
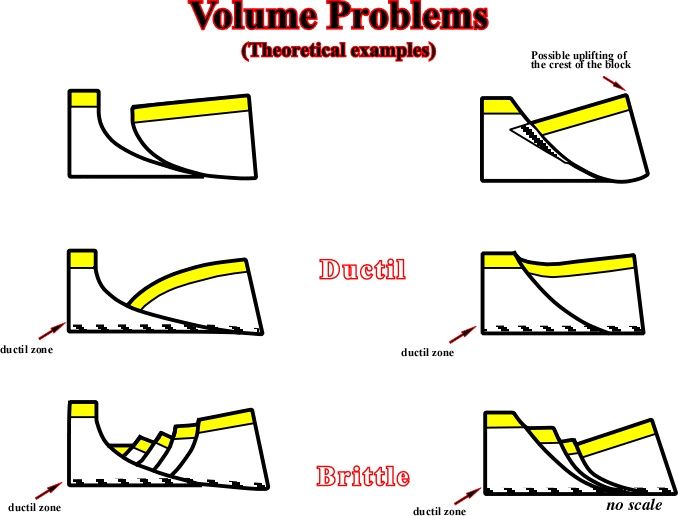
Fig. 105- These types of deformation are often observed when faulting becomes less active in a ductile layer within the sedimentary section (shale, salt, etc.).
Dominos: Rotated blocks along planar faults (fig.106):
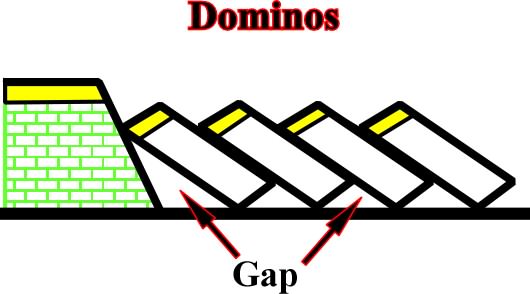
Fig. 106- Dominos are characterzed by no relative dip rotation between faulted blocks and by the fact that some mechanism is required to accommodate the space at the footand the end of the each block (gap).
Listric Faults: Fault trajectory concave upward (fig.107):
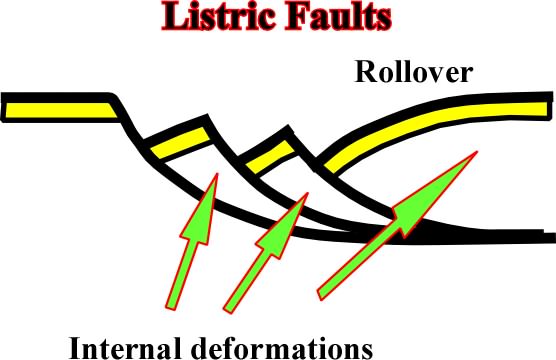
Fig. 107- A listric fault (from Greek "listron", i.e., "shovel") implies a rotation of the hangingwall, which controlled, or is controlled, by the depth of the detachment plane. As we will see next, the depth of the detachment can be predicted from the geometry of the rollover of a growth fault (fig. 108).
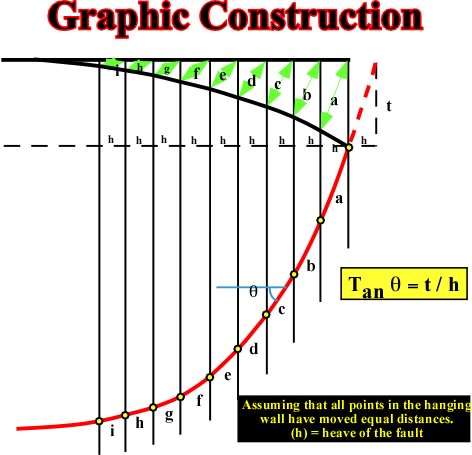
Fig. 108- Knowing: (i) the geometry of the hanging wall rollover, (ii) the heave (h) and assuming that it is the same for all points, (iii) the distance t, between each point of the rollover and the horizontal, one can calculate graphically the tan f as equivalent to t / h. Each value of tan f gives a, b, c, d, etc. The values a, b, c, d, e, etc., are then projected between the vertical of each considered point in the hanging wall, as illustrated hereunder.
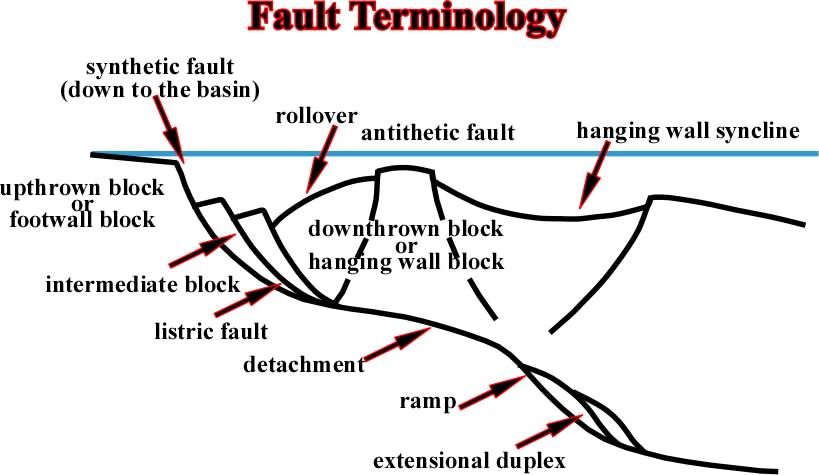
Fig. 109- In extensional tectonic regimes a esoteric jargon is often used, particularly by Anglo-Saxon geolgists. As depicted above the chiefly words are: (i) Synthetic faul, (ii) Upthrown bloc or footwall, (iii) Rollover, (iv) Anthitetic fault, (v) Hangingwall syncline, (vi) Downthrown block or hangingwall, (vii)Intermediate clock, (viii) Listric fault, (ix) Detachment, (x) Ramp, (xi) Extensional duplex, etc.
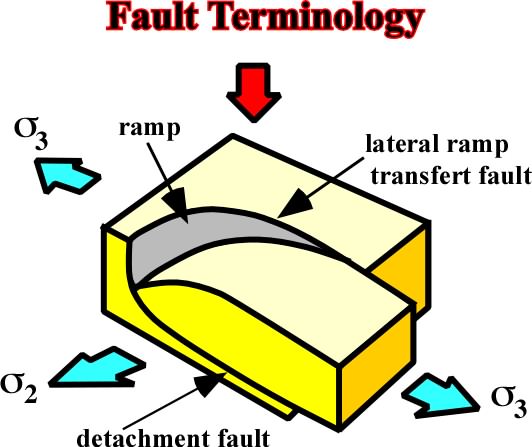
Fig. 110- A growth fault is a listric fault active during sedimentation and, generally, with a shallow detaching. The throw increases with depth and the strata of the downthrown side are thicker than the correlative strata of the upthrown side. A detachment plane, a ramp and a lateral ramp (or a transfert fault) are often used ti characterized part of a whole growth fault,
4.3.8- Development of Hangingwall Syncline
The hanging wall syncline's development is a direct consequence of a volume problem, i.e., of the Goguel's Law, as illustrated in the sketches below.
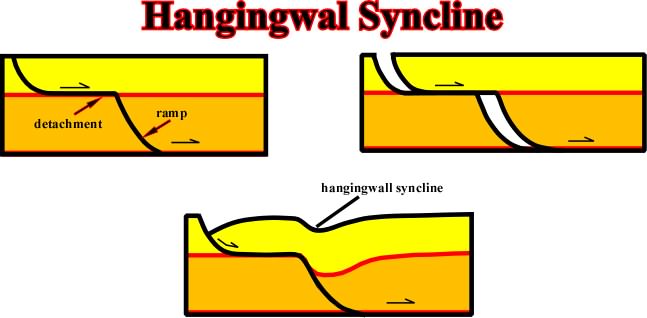
Fig. 111- As illustrated, it is evident that a hangingwal syncline is an extensional structure and not a compressional structure. It is associated to the lengthening of the hangingwall in order to respect the Goguel's law. The displacement of the hangingwall creates potential voids and so the sediments must accommodate to the new volume conditions.
4.3.9-Fault Intersection on Maps and Seismic Sections
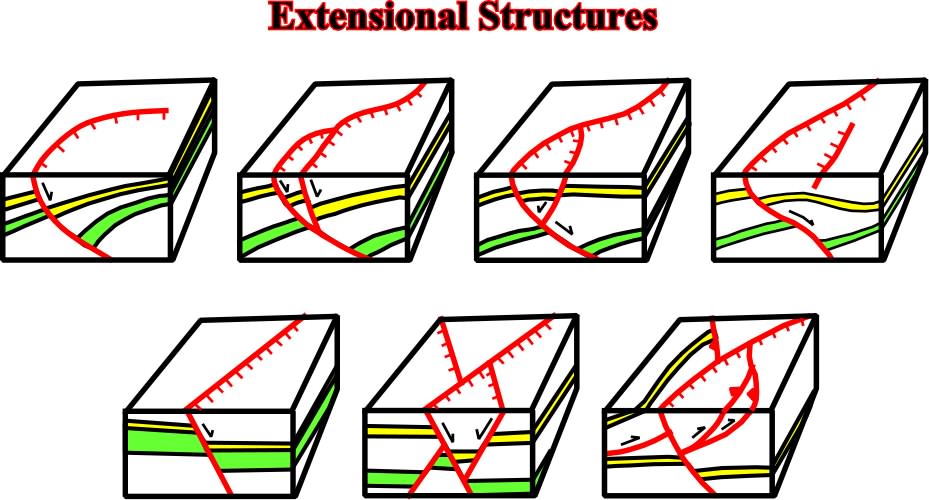
Fig. 112- The relationships between eroded surfaces, subcrop maps or seiscrops (all with flap topography) and the correlative cross-sections or seismic profiles are quite illustrated on these blocks diagrams. The geometry on the cross-sections or on seismic lines must match with the geometry on the flat surfaces. When a seismic interpreter recognizes a curvilinear normal fault on a seiscrop, the fault on a seismic profile must show, in depth, an increasing hade, i.e., its fault plane must flat in depth. Similarly, when two rectilinear normal faults intersect, on a flat surface, as well as on a cross-section, the youngest fault displaced the oldest. This hypothesis, which is only valid when the map (upper surface) is without or with a flat topography, is illustrated by two the lower right blocks.
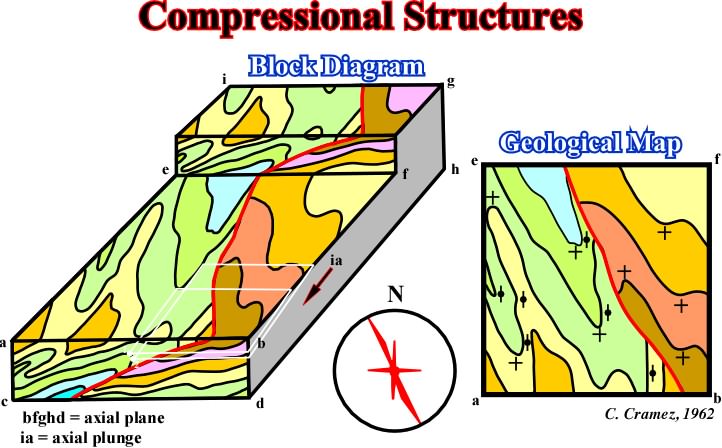
Fig. 113- The relationships observed in extensional structures (fig. 112) between horizontal surfaces (geological maps without topography, or seiscrops) and cross-sections (or seismic lines), must also be respected on compressional structures, particularly in those deformed by concentric folding. These relationships are summarized in this block diagram, in which the basic principles of 3D seismic interpretation are depicted. The strike of the more dipping beds gives roughly
This block diagram clearly illustrates that in a concentric folding (hydrocarbon domain):
(i) The direction of the axial plane, i.e.
(ii) The axial plunge is given by the dip of the lesser dipping beds.
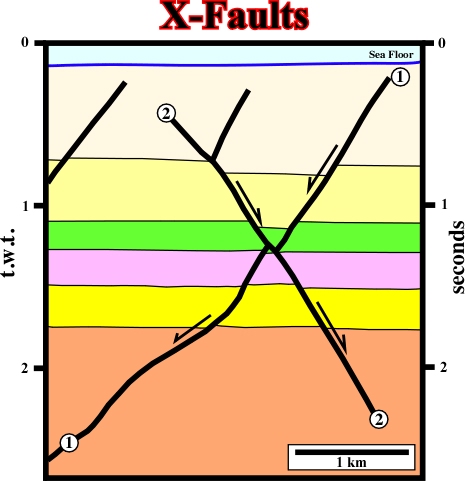
Fig. 114- This seismic line from Gulf of Mexico, illustrates a typical example of normal faults in X. The younger fault, dipping to the right, offsets the older on which dips to the left. In a seiscrop , or in a flat geological map, also the younger fault displaces the older one. However, as we will see below, in a time structural map or in a geological map with a significant topography, that is quite more complicated.
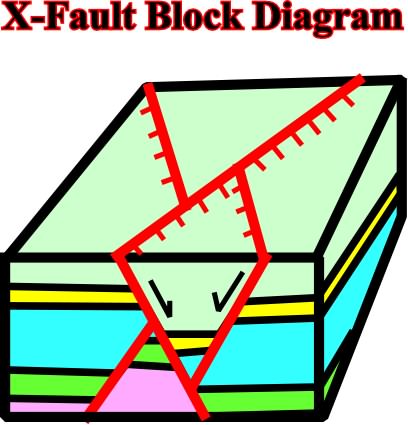
Fig. 115- In a cross-section ( or seismic line) the intersection of the normal faults X faults) are characterized by a graben structure overlying, in the same vertical, an horst structure., as illustrated on this block diagram and on the seismic line illustrated on fig. 114. The mapping of these faults depends on the level of cartography. In upper levels the mapping is relatively easy. We just need to make a dextral rotation of rotate 270° to get the geometry on the ground surface. However, as we will see in the next, the influence of the topography (see fig. 117) is quite important.
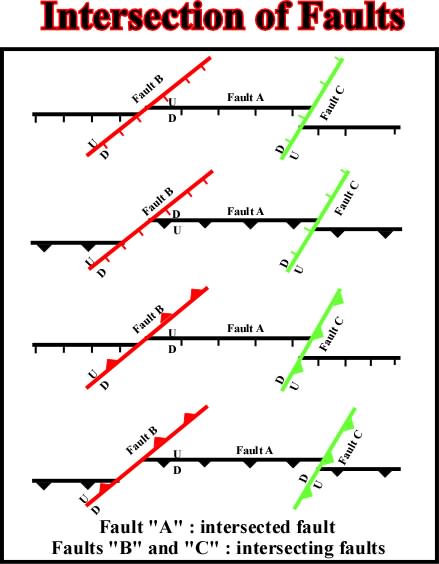
Fig. 116- This map illustrates various combinations of faults intersecting at different angles on a planar surface or on a non-conformity. The intersection of the intersected fault (in black) and the surface is invariably offset by the intersecting faults (red and green) in the direction of its dip in the upthrown block. This offset is independent of the intersection angle of the faults, providing the direction of movement of the intersecting fault is dip slip.
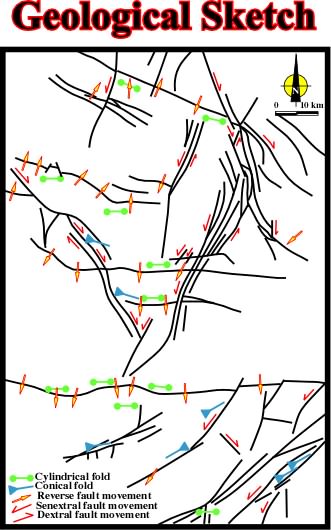
Fig. 117- On this geological sketch, it is evident that the sediments were shortened by compressional tectonic regime characterized by a
b) Subsurface or isochrone seismic maps.
The effects of intersecting faults on subsurface or isochron seismic maps are much more complicated than on a flat surface. Two intersecting faults cutting the beds into four blocks which vertical displacement can be very different for each block. In the maps the later fault is apparently displaced by the earlier one as illustrated in the block diagram hereunder.
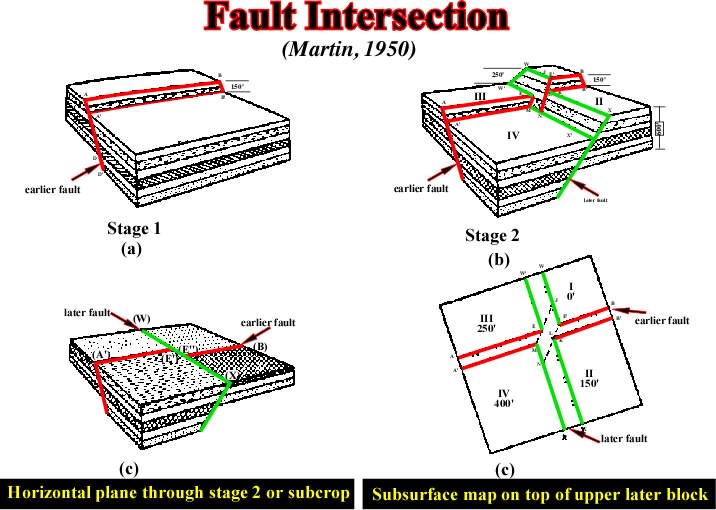
Fig.118- Very often explorationists, when interpreting isochrone maps (time structural maps) do not take into account influence of the topography this possibility , i.e. time contour maps of deformed chronostratigraphic surfaces. In fact, on these maps, as a consequence of the topography, often younger faults are apparently offset by older faults.
The understanding of such a displacement is extremely important in order to establish the faults' chronology which is fundamental to evaluate the probability of presence of hydrocarbon in certain non-structural traps, such as morphologic. Indeed, as in all other traps, the age of the trap must be necessarily older, or synchrone, of the hydrocarbon's hydrocarbons.
to continue press
next
Send E-mail to ccramez@compuserve.com or cramez@ufp.pt with questions and comments about these notes.
Copyright © 2001 CCramez
Last update: March, 2006