

11) Volume Problems (Goguel's Law)
When interpreting, in geological terms, a seismic line, do not forget, that the amount of sediments must be kept, more or less, constant.
Geology is systemic. Volume problems cannot be understood in isolation. The understanding of volume problems should progress from general (whole) to particular (part). A geologist understands, correctly, an individual structure (compressional or extensional) just when he understands the complete system. This is particularly true when he tries to interpret seismic lines in fold-belts or shortened backarc basins as in the geographic Neuquén Basin. A geoscientist (or seismic interpreter) working in such basins cannot start to pick seismic markers or fault planes, in continuity or not, and hoping that a coherent geological model will appear at the end.
- Naive inductive seismic interpretations do not exist.
- The theoretical framework within which geoscientists work is critical to observation and picking.
- There is no legend on seismic lines telling geoscientists what they should look for.
- To identify reflections and seismic surfaces, geoscientists must know what they should look for.
- If this sounds somewhat circular, and it is, it explain why scientific exploration progress is difficult.
In Geology, and particularly in Petroleum Exploration, ground rules concerning volume preservation during deformation have been used for a very longtime, such as:
(i) Incompressibility of rocks ;
(ii) Dissolution ;
(iii) Erosion ;
(iv) Salt and shale tectonics ;
(v) Folding and Faulting ;
(vi) Facies ;
(vii) Dissolution ;
(viii) Compaction.
The better or preferable tentative geological interpretation will be correct, more often, than the more improbable one, seems evident but it is not. The idea of corroboration, or degree of corroboration, was introduced by certain philosophers of sciences, with the aim of showing clearly that every probabilistic theory of preference is absurd. In fact, at a certain time (t), the degree of corroboration of a geological hypothesis is the report evaluating the way it stood up to critical tests. Corroboration is an evaluating report of past performance. It says nothing whatever about future performance, or reliability of the hypothesis. Do not try to corroborate a tentative interpretation try to refute it.

Figure 044- The seismic line is perpendicular to the structural trends, which are mainly associated with cylindrical folds and thrust faults. The tectonic regime responsible of the shortening was characterized by an σ1 horizontal and σ3 vertical. Consequently, theoretically, there are not significant lateral displacements. The proposed tentative interpretation (A) looks quite plausible. However, it does not resist a critical discussion. A simple restoration test (see the sketch on the right of the figure) refutes the proposed tentative interpretation. The geoscientist in charge of the interpretation did not respect the volume preservation during deformation (Goguel’s law). A restoration test has nothing to see with an automatic flattening of a seismic marker, in which the geometrical relationships, between the seismic marker, are, partially, destroyed and the volume of the sediments is not preserved, what is against the Goguel’s Law : “during deformation (salt and shale tectonics excluded), the volume of the sediments is preserved, taking into account, compaction and dissolution”. Indeed, for each kilometer perpendicular to the profile, a volume of some 16 km3 disappeared in depth. As a consequence, the geoscientist is obliged to advance another tentative solution, i.e., another geological interpretation of the seismic line, which, at least, must resist volume problems. At this point, it is relevant to point out, again, that interpretation progresses by tentative solutions (trial and error). Seismic interpreters cannot accomplish their job just performing a single tentative interpretation of the seismic data. Often, they are quite surprised noticing that in the second or third tentative interpretation they see many more geological event in the data. Again, never forget that observations are theory-laden.

Figure 045 - This picking of the main seismic reflectors comes from a seismic line, in which there is not significant lateral displacements. The proposed picking clearly points out that the interpreter forgot that during deformation the volume of sediments must, more or less, be keep, constant (porosity reduction and stylolite formation taken into account). Such interpretation does not resist a simple geometrical critical test. Indeed, the shortening of the seismic markers is not coherent. The green marker (C), for instance, is much more shortened that the red marker (A). Therefore, some kind of detachment plane or tectonic disharmony must be present. In fact, the geometric relationships between the seismic markers can only be explained by a tectonic inversion, in which the old normal faults were reactivated by a compressional tectonic regime or by a tectonic disharmony characterizing different styles of tectonic deformation.
In these notes, just the incompressibility of rocks will be taken into account, since it is in this matter, that the majority of the tentative geological interpretations of the seismic line, that I saw in my last trip to Argentina, are easily falsified, particularly due to the fault picking. Using the figures 044 and 045, taken from other exploration areas, you can say, at structural stand point, geoscientists must to be able to change every tentative geological interpretation to propose its original state, without violating the rule of volume preservation (Goguel’s law), taking into account the more likely exceptions : (i) Dissolution ; (ii) Erosion, (iii) Salt basins, etc.
For that they should not forgot that volume problems created by extension, for instance, can be solved in normal faulting by two different ways, as illustrated below (figure 046).
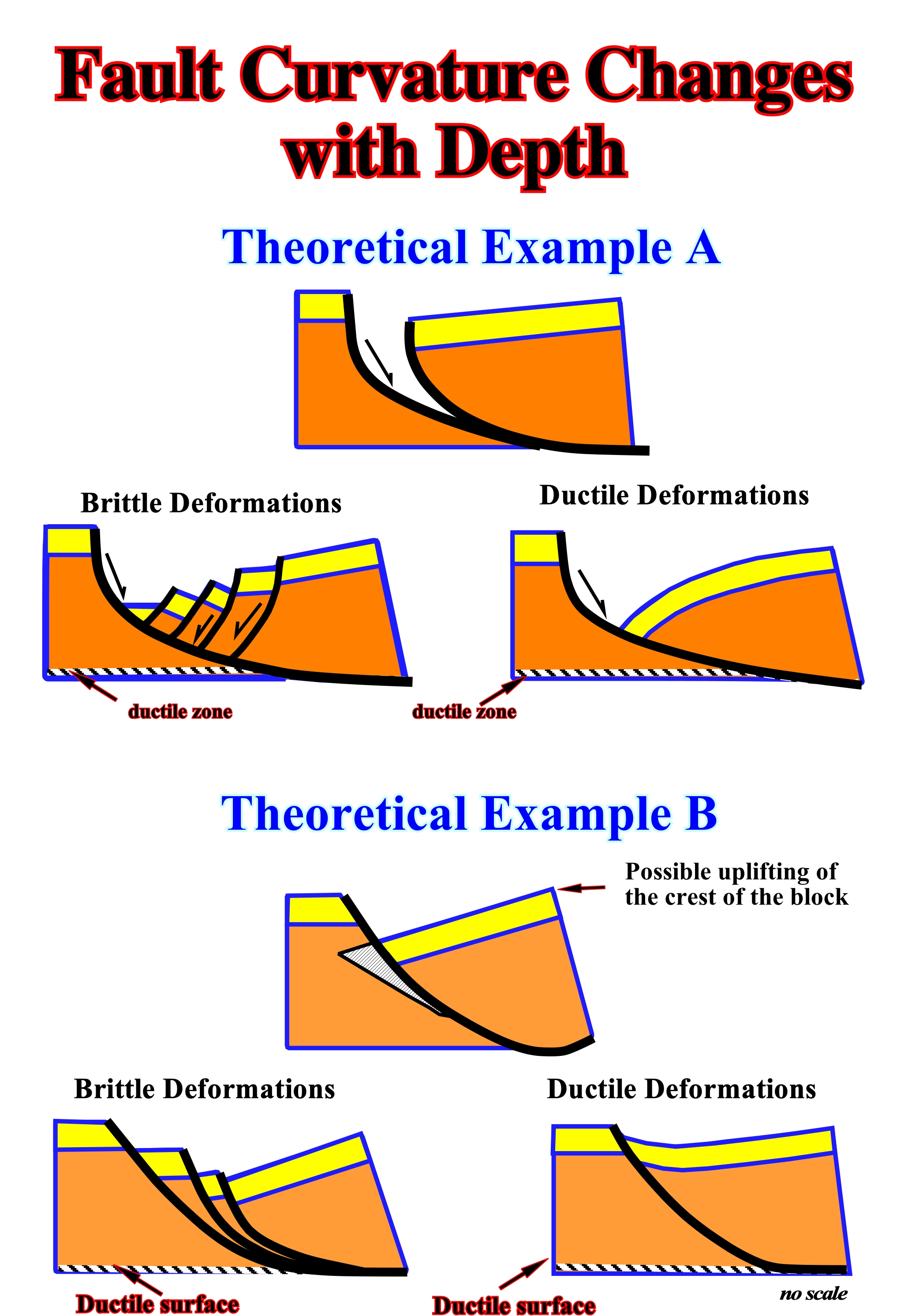
Figure 046 - When the geometry of the fault plane is curved, to avoid a potential void, the sediments are lengthened by antithetic normal faults dying in a major synthetic curved fault limiting the hangingwall in downdip direction (brittle material). When sediments are ductile, faulting is quite limited and, in certain cases, absent : a rollover, in the hangingwall, solves the volume problem. In this geologic model, the volume problems of curvilinear faults (in surface and depth) is solved either by synthetic listric faults : (i) several drag-faulted blocks (riders), when sediments are brittle or (ii) by a synform, when sediments are ductile.
In the theoretical example A, the geometry of the fault plane creates a potential void when the hangingwall is displaced forward and the sediments are lengthened to fill the space created. The lengthening mechanism depends on the rheology of the sediments: the accommodation will be different if the sediments are brittle or ductile. In the theoretical example B, the geometry of the fault plane is such that when the hanging-wall is displaced to allow lengthening, there is (theoretically) an overlap between both faulted-blocks, which can be solved in two different ways illustrated below.