Universidade Fernando Pessoa

Porto, Portugal

Volume Problems
in
Real Crustal Deformation

II- Tectonic Regimes & Volume Problems

a) Foreword

Theoretically, when the maximum effective stress (1) is horizontal, sediments are compressed, that is to say, shortened, which implies uplift and subsequently (i) a relative sea level fall, (ii) erosion and (iii) an unconformity (Fig. 38). Contrariwise, when 1 is vertical, sediments are extended, i.e., they are lengthened, which implies subsidence and subsequently (i) a relative sea level rise and (ii) sedimentation (Fig. 38).

Fig. 38- In a compressional tectonic regime (1 horizontal), sediments are shortened by folding and/or reverse faulting. Apart from the exception discussed previously, during deformation the volume of sediments stays more or less constant. Similarly, in an extensional tectonic regime (1 vertical), sediments are lengthened by normal faulting with volume preservation. From these geological conjectures, is obvious that a compressional regime postdates always an extensional regime. Indeed, it is impossible to shorten sediments before depositing them. The ensuing geological events following compression or extension are completely different as indicated in the above sketches. Therefore, geologists must avoid taking compression as extension or vice versa. On the other hand, it is important to notice that both sequences of geological events are used to criticize of the tentative solutions. Let's see an example. Suppose that explorationists, i.e., a geoscientists working in hydrocarbon (oil or gas) exploration, must solve the following problem: In the offshore, and particularly on the area covered by seismic, what are the expected traps? The explorationist, after advancing the more likely tentative solutions, using the global and regional geological settings of the area and his past experience, is going to criticize them using the seismic data. Knowing the problem he must solve, he can start to observe the seismic data in order to exclude the tentative solutions easily refuted. The first step of observation is crucial. Indeed, he must start to decide whether the sediments (in this case seismic reflectors) are lengthened or shortened. If he makes a mistake in this first step, the sequence of geological events that he must look is completely different and for sure the answer to question will be wrong. Indeed, it is quite frequent see antiforms (extensional structures) interpreted as anticlines (compressional structures) and morphological traps by juxtaposition interpreted as structural traps, etc. The result of initial mistake is always the same, i.e., dry wells, excepted when oil is found by serendipity, but this is another story (quite common, by the way).

A relative sea level rise (RSL) increases accommodation and whether a transgression or a regression takes place depends on the velocity of the RSL. Indeed, when the sea level rises in acceleration a transgression takes place. When it rises in deceleration a regression takes place. In fact, associating a transgression with a relative sea level rise or a regression with a relative sea level fall is incorrect: shallow water sedimentation always implies an increasing of the space available for the sediments, that is to say, an increase in accommodation.

b) Volume Problems in Compressional Tectonic Regimes

The volume problems discussed here concern mainly those created by concentric folding, in which the thickness of beds, when measured perpendicular to bedding planes, is more or less constant (fig. 39). Due to preservation of volume (Goguel’s law), the geometry of the fold changes with depth. In the photograph below (fig. 39), it is easy to recognize that the morphology of the folds changes in depth and at the level of less compactable beds. The understanding of volume preservation in the core of anticline structures and what it can solve is quite important, particularly in hydrocarbon exploration, where large oil and gas fields are quite often associated with anticline structures (Fig. 40).

Fig. 39- The description and classification of fold geometry given in most text is restricted to the fold profile section, probably because they are assumed to be cylindrical, that is to say, that its profile does not change along the fold hinge. However, field observations and experimental works indicate that this is generally not so. Due to preservation of volume (Goguel’s law), the geometry of the fold changes with depth, as illustrated on this photograph. Indeed, the morphology of the folding changes not only in depth but at the level of less compactable beds as well. Indeed, as said previously, and as we will see next, the understanding of volume preservation in the core of anticline structures and what it can solve is important in hydrocarbon exploration, in which the majority of oil reserves are trapped in anticline structures (Fig. 40).

Fig. 40- Around 60 Ma ago, the Wind River sediments were shortened and uplifted, creating large petroleum structural traps. Lander oilfield is one of Wyoming’s sites where commercial oil has been exploited since 1884, in an anticline structure. This field has produced over ten million barrels of oil since its beginning over 100 years ago. The oil was generated in the Chugwater, Phosphoria, and Tensleep Formations, two of which are visible in Red Canyon. The Lander Oil Field, in the Wind River Basin (Wyoming), is a typical example of an apparent structural trap (“four way dip”) associated with an anticline structure. On the surface, the structure looks quite simple. In depth, due to volume preservation, the structure becomes very complicated. At the level of the reservoir-rocks, the trapping seems to be morphologic by juxtaposition and not structural (± four way dips). The seismic lines seem to indicate that the volume problems were partially solved by opposite reverse faults. In fact all anticline and particularly concentric anticlines, in depth, due to the volume problems created in the core, are considerably complicated for the reasons that we will discuss next.

b.1) Volume problems in the core of an anticline

As said previously, different hypotheses have been proposed to solve the volume problem created in the core of anticline structure (Fig. 41). The majority of geologists agree that they are filled up by shortening of the sediments.

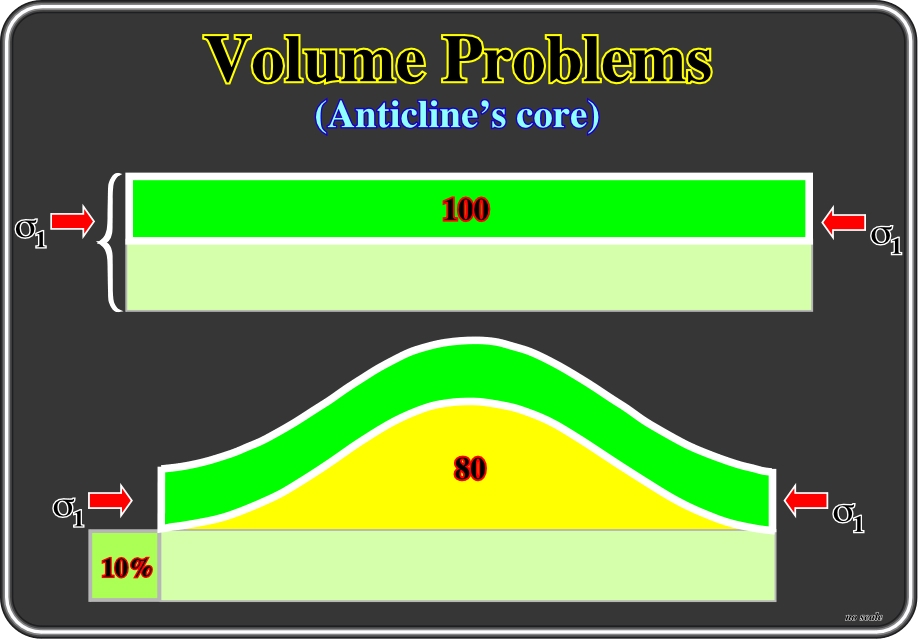
Fig. 41- Let's consider the superposition of two isopachous beds composed of material with different rheologies. The upper one is composed by rigid or brittle material, while the lower one is composed by a ductile material. Under a small stress condition, both beds will be shortened, (for instance 10%) but by completely different mechanisms. The volume lost (in this case the area) in the lower ductile horizon (light green) corresponds to the little square at the left-hand side of the section (10%). The upper bed keeps its volume the same but is shortened by folding which creates a volume, that is to say, an empty space, in the core of the anticline. The volume lost by the ductile bed does not compensate the volume created by folding. In fact, it is eight times the area of the square reduced by shortening. Therefore, shortening by folding of such a sedimentary package is volumetrically unlikely. A ductile material is able to sustain, under a given set of conditions, 5 to 10% deformation before fracturing or faulting. A rigid or brittle material folds or fractures at less than 3-5% deformation or strain. Intense ductile deformation of rock usually takes place at considerable depth in the Earth’s crust where the temperature and confining pressures are high or before sediments have been completely indurate.

The key hypotheses are:

a) Folding and thrusting of basement;
c) Crushing of basement;
d) Flowing of mobile layers;
e) Disharmonic folding in the heart of the anticlines.

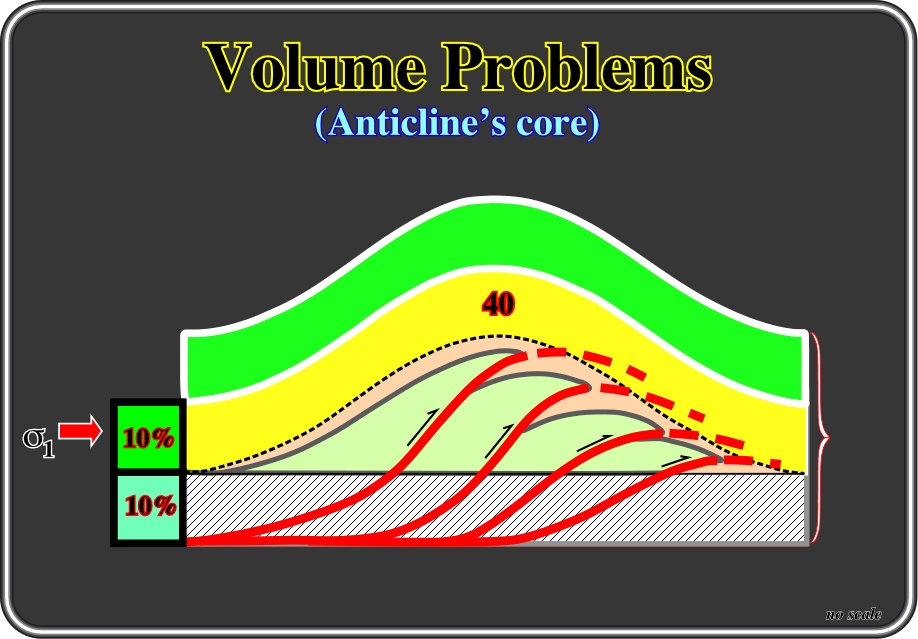
Fig. 42- As illustrated in this sketch, by doubling the thickness of the layers shortened and filling the core of the anticline structure by thrusting the substratum, not much is gained towards balancing the volume deficiency. The area created in the core of the anticline still is four times higher than the volume gained by shortening.

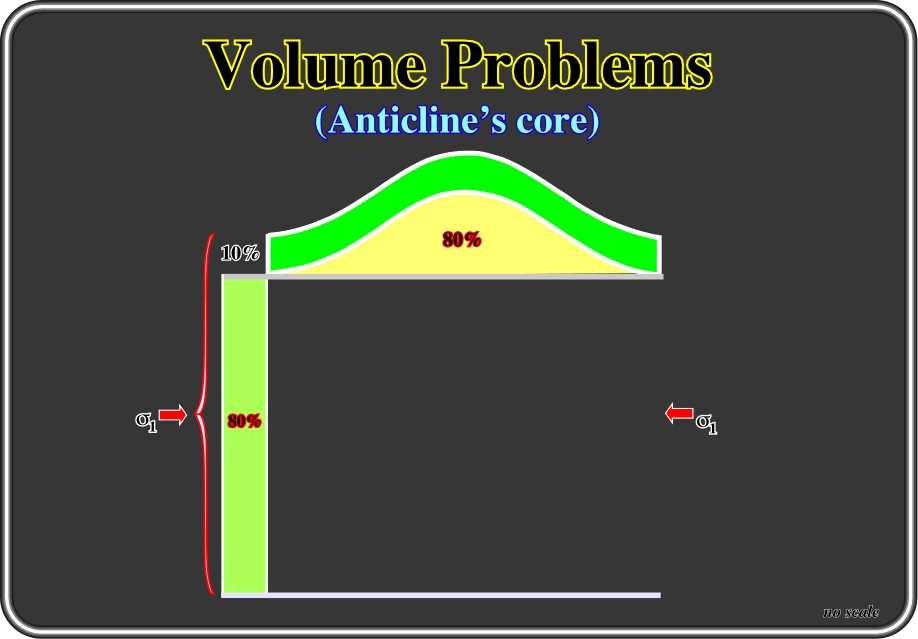
Fig. 43- Theoretically, in order to fill the core of the anticline illustrated in fig. 41, one would have to compress a ductile layer eight times as thick as shown above. In spite of the fact that such a tentative solution looks rather unrealistic, it is volumetrically correct.

Fig. 44- A more plausible solution to the volume problem in the core of the anticlines, but not recognized by all geologists, can be achieved through the filling of the anticline core by material that has been borrowed from the synclines. Such phenomena are evident in salt pillows, and it is probably also true for many décollement folds, in which the growth of the anticlines can continue until all the ductile material underneath the syncline is consumed. However, after the consumption of the ductile material, a more complicated style of folding, combined with faulting, will ensue. Notice that in the lower sketch, the true thickness of the original ductile horizon is therefore present only in two points of this section, which leads to considerable difficulties in constructing isopach maps of ductile horizons involved in folding.

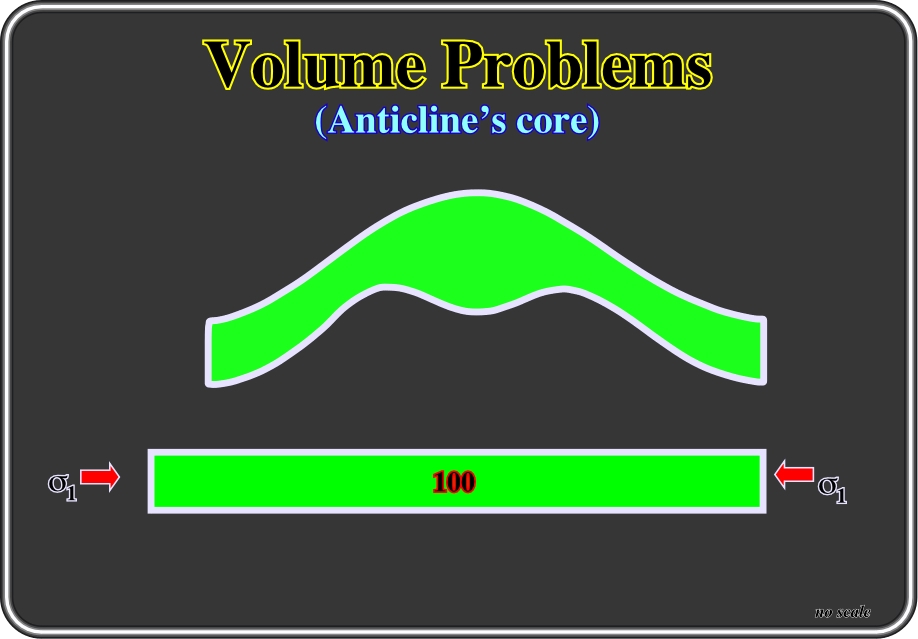
Fig. 45- The same principle of preservation of volume (or area, in the strike cross-sections) should also be observed in inharmonious (or disharmonic) folding, that is to say, when the beds have different strength, particularly if one is a highly mobile layer (Stille, H., 1925). In this example, not only the lengths of the two boundaries are preserved, but also the area enclosed within them. Mobile or under-compacted sediments can flow from synclines toward the heart of anticlines in order to solve void potential or volume problems.

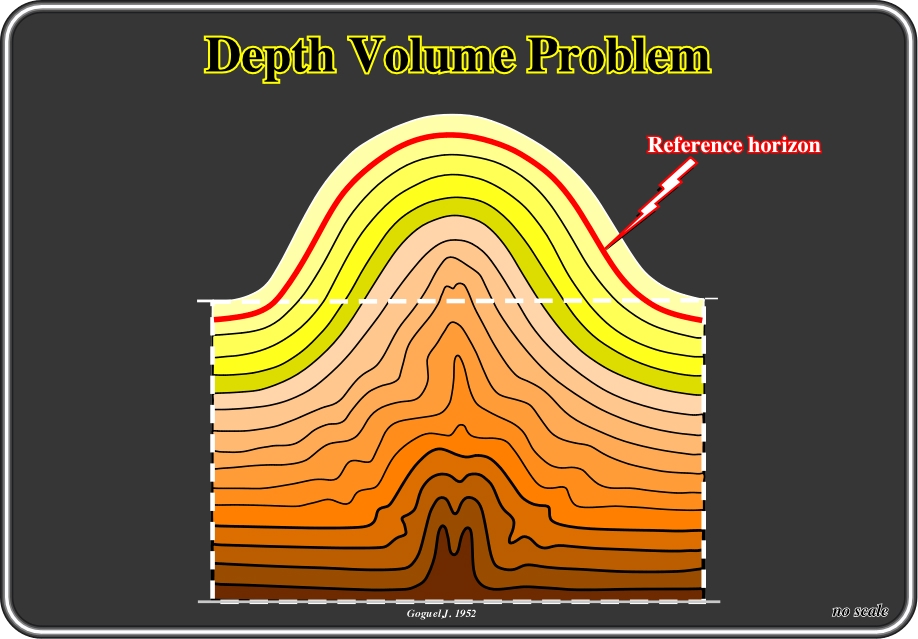
Fig. 46- In 1952, Goguel proposed a disharmonic folding, in depth, to preserve the volume in concentric anticlines, where the development of smaller and disharmonic folds, in the core of the anticline, can solve volume problems over a detachment surface. In fact, geometrically, when on the basis of the curve of a given sedimentary horizon, plotting the parallel curves, it arrives at a moment that a common centre of curve is reached, from which downward the plot presents two points and two crossing branches. Physically, it is impossible that such a plot corresponds to the shape of the sedimentary beds. In fact, in concentric folding, after a certain moment, as depicted in Goguel's sketch above, it is necessary that the assumption of conservation of thickness (volume preservation) cesses to apply. Beds for which the thicknesses are not preserved create what geologists call a disharmony, since the geometry of the folds above and below are quite different.

Symmetrical overthrusting of an anticline’s flanks over an axial depression in the tightened core zone of the anticline allows persistence of concentric folding (Fig. 47). Such a way to accommodate sediments to the new volume conditions is difficult to recognize on the ground, but not on deep parts of seismic lines, as illustrated next.

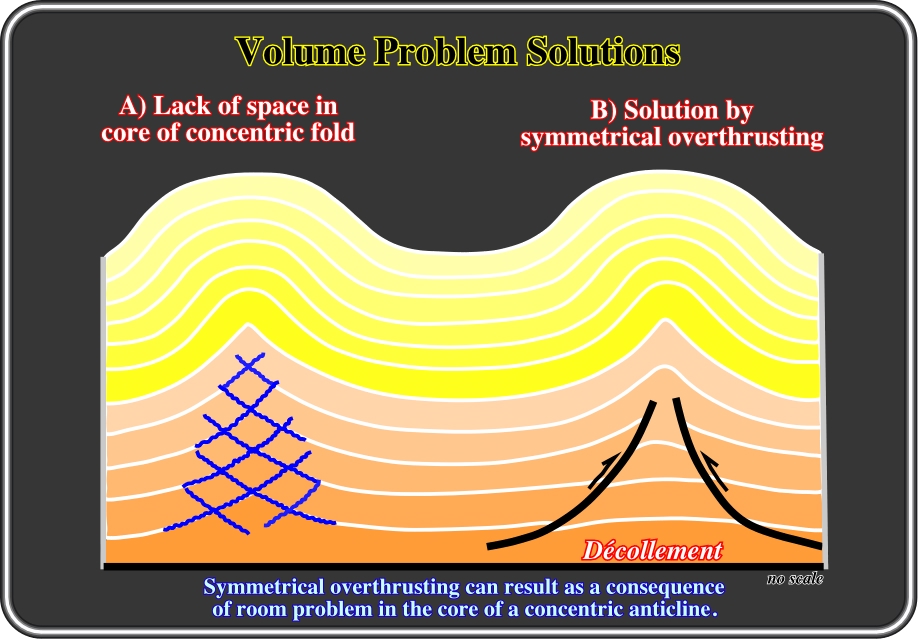
Fig. 47- Two possible ways to solve volume problems in the core of anticline structures are illustrated in this sketch: (i) Disharmonic (or inharmonious) folding, which occurs mainly in heterogeneous sedimentary sequences with ductile layers alternating with rigid or brittle layers, and (ii) Opposite reverse faults, which occur rather in more or less homogeneous sedimentary sequences. Both potential solutions are observed on the ground and on seismic lines. Disharmonic folding is recognized rather at relative small scale (mesoscopic scale, i.e. at the scale of outcrops), while opposite reverse faults are observed mainly at macroscopic scale (scale of geological maps or seismic lines). The accommodation by opposite reverse faults is well documented in fold-belts and tectonic inversions. However, in fold belts, due to volume reasons, the opposite reverse faults flatten in depth and die on subhorizontal décollement surfaces (figs. 48 and 49). In tectonic inversion, the opposite reverse faults are old normal faults reactivated with a reverse movement during the compressional tectonic regime.

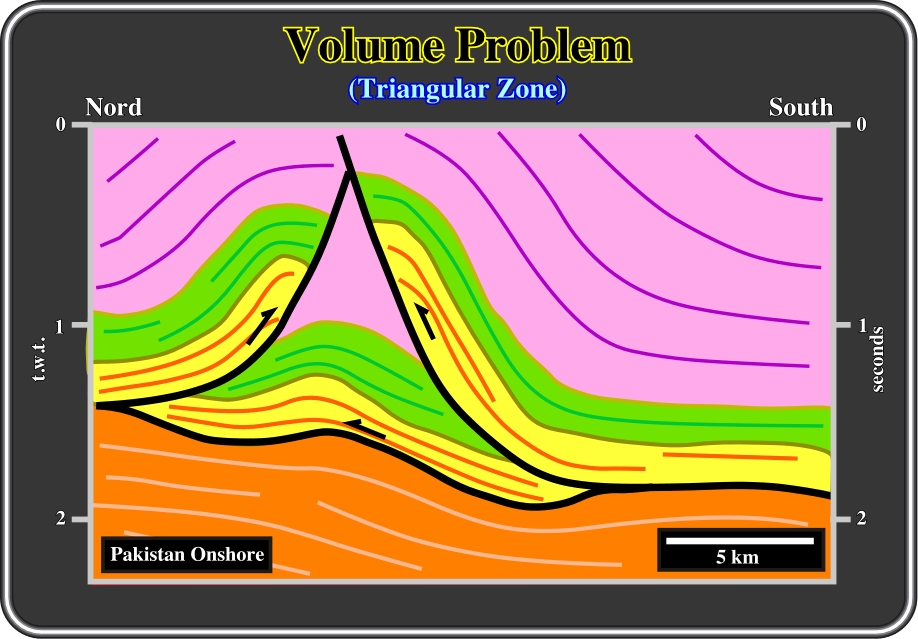
Fig. 48- In onshore Pakistan, particularly in the Khorat fold-belt, volume problems in the core of anticline structure are often solved by symmetrical thrusts that flatten and dye in a major detachment surface, as illustrated on this interpretation of a seismic line of the area. Indeed, as depicted above, in the upper part of the line, as on the geological map, deformation is simple: relatively narrow anticline structures and rather wide synclines. However, in depth, the seismic data suggests a much more complex deformation since volume problems are more important. Notice that this tentative solution is reductionist. The complete system is not shown, and so, isolated seismic tentative solutions are difficult to test. Indeed, quite often, they can be considered as metaphysical solutions since they cannot be falsified (refuted).

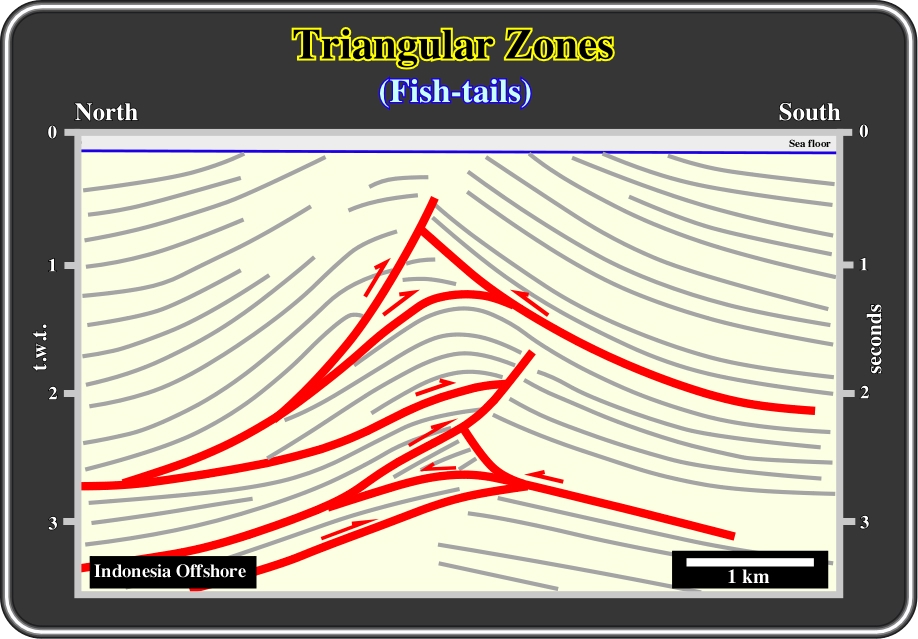
Fig. 49- This structural interpretation of a seismic line from a back-arc basin (northern Lombok offshore in Indonesia), illustrates how, in a concentric fold, simple surface anticline structures overlie complex thrusted and faulted structures. As depicted, overthrust anticline flanks, with opposite vergences, often form triangular zones ("fish tails”), dying in major basal décollements or detachment surfaces. As said previously, such compressional structures were developed to accommodate the sediments to new volume conditions created by shortening. Admittedly, different levels of deformation can be considered and is not forbidden to speak in “Stockwerk Tectonics”. Indeed, different petroleum traps, associated with different structures, are stacked, which is rather interesting in petroleum exploration.

b.2) Décollement surfaces

In a concentric fold, in depth, folds and the associated thrust faults must die on décollement or detachment surfaces. Otherwise, they cannot be balanced (equilibrated or restored), as illustrated in fig. 50.

Fig. 50- These sketches put forward that a concentric fold cannot be balanced without detachment surfaces. Assuming the geometry and amplitude of the folds decrease in depth, without any major discontinuity, as depicted in A, one can say the upper beds are more shortened that the lower ones, which is physically impracticable. Indeed, restoring A to B creates void problems in depth. Such a problem can be difficult to solve, particularly when the line is only one view of a large system, as is the case in this example. However, generally, geologists never try to solve problems of this kind in isolation. Admittedly, in this particularly case, without a fixed point in the foreland all restoration will be meaningless. The lower sketch (C) illustrates a potential tentative solution, in which a décollement surface separates two realms of deformation. The underlying sediments are almost undeformed, while the overlying are shortened by concentric folds and reverse faults that flatten, in depth, and die on the décollement surface (see fig. 51).

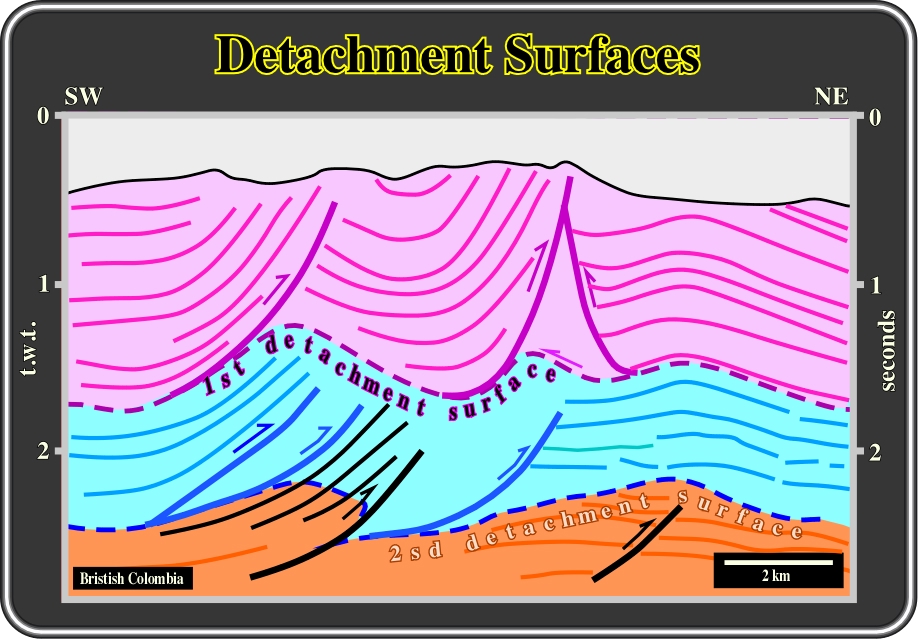
Fig. 51- In the British Colombia foothills deformation is post-depositional and it progresses towards the craton. The shortening is in sequence and so, several levels of deformation bounded by décollement or detachment surfaces are present. In this interpretation of a seismic line of the area, the deeper the décollement surfaces the younger they are. To solve volume problems within each deformation level, cylindrical folds, thrust faults and triangular zones must be identified. In this particular line, two detachment surfaces (purple and blue) are recognized and a deeper one can be predicted (out of the section) by the black thrusts faults. As said, the oldest décollement is the shallowest. The purple thrust folds die on it. In addition, it is deformed by younger thrusts associated with the blue detachment surface. This visible deeper detachment surface is folded and faulted by thrusts (coloured in black), which must die in a deepest and youngest detachment surface, which can be predicted but not picked on this seismic line.

Geologists grounded in Goguel's concepts easily found how to predict the depth of décollement surfaces. Indeed, under a compressional tectonic regime, sediments are shortened, which implies uplift to preserve a more or less constant volume. Subsequently, one can say that the volume created by uplift, as illustrated in figure below, balances the volume lost by shortening.

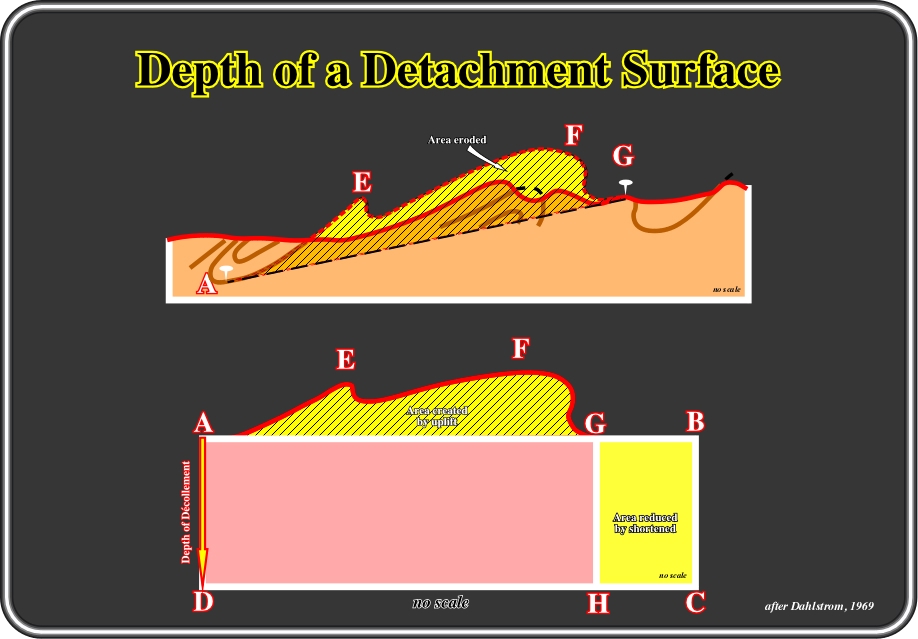
Fig. 52 - The depth of the detachment surface (AD) can be calculated knowing the excess or uplifted area (AEFG). According to Goguel’s law, the area reduced by shortening (GBHC) must be more or less equal to the uplifted area (AEFG) which allows for prediction of the depth of the décollement as illustrated in the figure below.

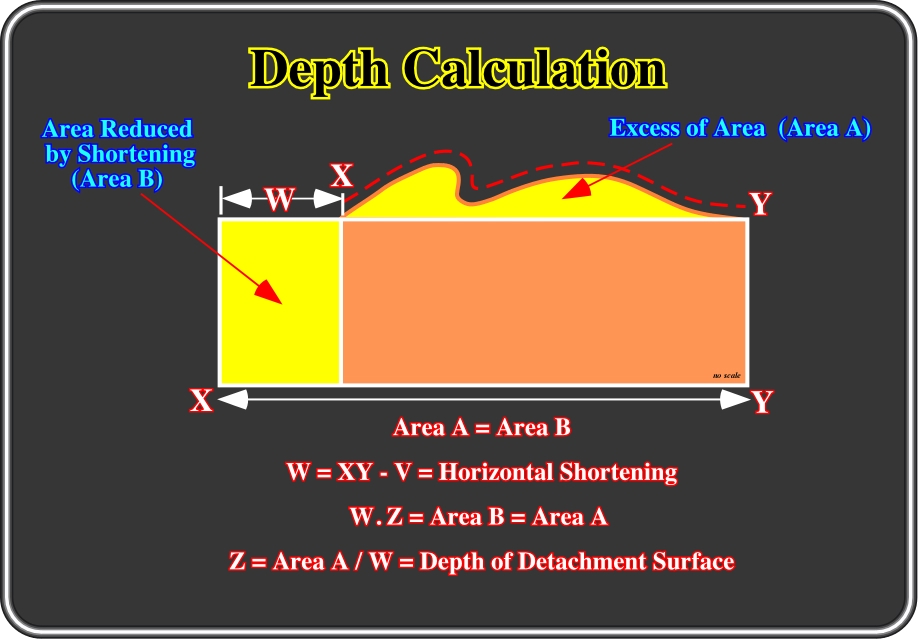
Fig. 53- The depth of a detachment surface (Z) is easily calculated by dividing the area reduced by shortening (Area B), or the equivalent excess or uplifted area (Area A), by the horizontal shortening (W). The horizontal shortening is the difference between the original length between two points and their length after shortening (folding). Swiss geologists attempting to determine the depth of the décollement surface in the Jura Mountains, as illustrated in fig. 54, successfully used this geometrical method.

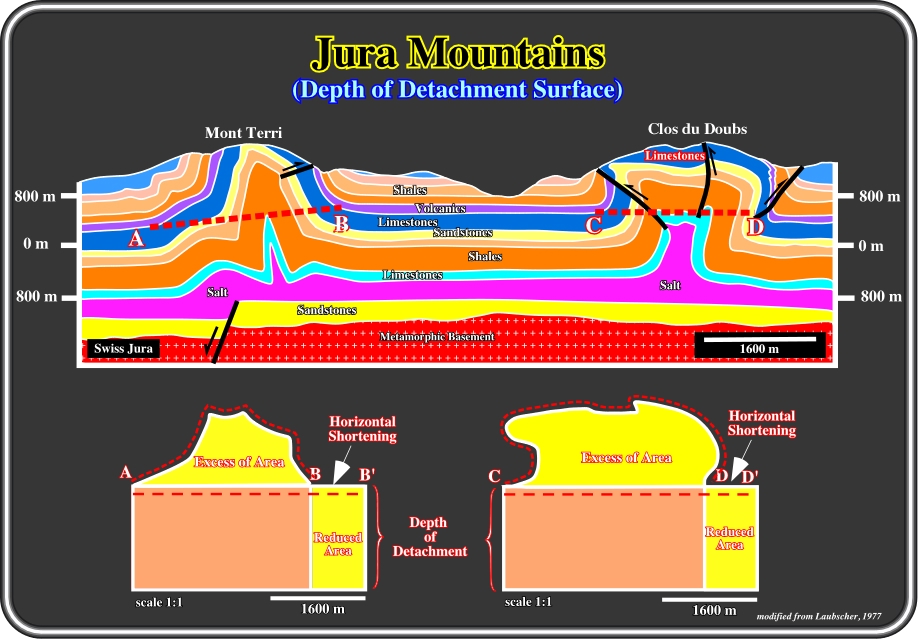
Fig. 54- In the Swiss Jura Mountains, Laubscher (1977), using the excess of area method, calculated the depth of detachment (more or less the top of the evaporites) as 800m below sea level. In fact, as said previously, the depth of detachment can be calculated dividing the excess, or the reduced area, by the horizontal shortening. The calculation of the excess of area was made using the uplifted areas of the small cross-section A-B and CD.

According to Dahlstrom (1970, 1990), depth detachment calculations assumes:
1) The existence of a décollement or detachment surface (except in basement uplift anticlines).
2) A constant tectonic transport in the ac plane, along the 3  (except in intra-cutaneous thrusting).
3) No significant flowage, in spite of the fact that a décollement requires always a certain amount of flowage.
b.3) Folding & Faulting Solutions

Three major different ways exist to solve volume preservation in compressional tectonic regimes (3 horizontal):

(i) Folding & Décollement;

(ii) Folding with Reverse Faults & Fault Reactivation;

(iii) Imbrications.

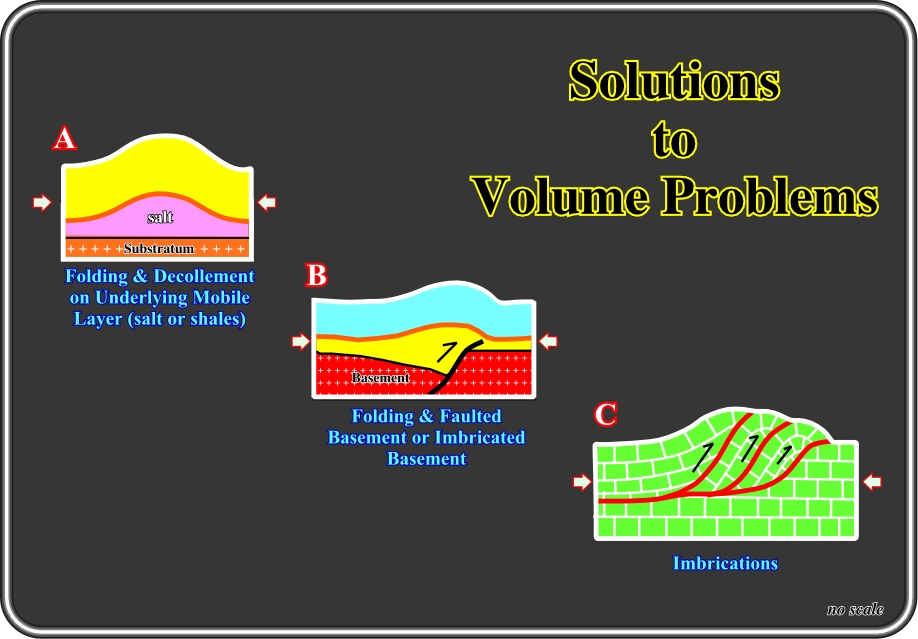
Fig. 55- Three different ways to respect volume preservation in compressional tectonic regimes are illustrated in this figure. In A, sediments and a mobile layer (salt) are folded above a rigid substratum. In B, during an extensional tectonic regime, sediments were lengthened by a normal fault looking leftward. Later, under a compressional tectonic regime, folding shortened the sediments and the pre-existent normal fault was reactivated as reverse fault. The fault reactivation was not too important. Its geometry, at least at the basement level still is that of a normal fault; however its movement was reverse, since the original vertical throw decreased. In C, the volume preservation is made by imbrications of the thrust faults.

Fig. 56- In this interpretation of a seismic line from the North Sea, the sediments (evaporites, in violet) were folded over a Paleozoic substratum. Salt flowage towards the core of the anticlines solve volume problems created in the heart of the structures. Salt flowage are easily recognized by thickness variations in the salt overburden. Notice that the apparent reduced thickness in the limbs of the anticline structures is due, as we saw previously, to the vertical exaggeration. By the same token, increasing thickness on the crest of the anticlines is apparent.

to continue press